 por Danilo » Ter Abr 23, 2013 11:51
por Danilo » Ter Abr 23, 2013 11:51
Calcular a derivada de

tentei fazer assim:
derivada de

=
![\left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right] \left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right]](/latexrender/pictures/4da6df81b35355fd2435511458c74605.png)
=

mas essa não é a resposta correta eu não sei onde está eu erro. E eu também não consegui colocar o símbolo de derivada.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Dúvida ao calcular uma derivada...
por dileivas » Ter Mai 01, 2012 09:54
- 2 Respostas
- 2266 Exibições
- Última mensagem por dileivas

Ter Mai 01, 2012 17:18
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] Duvida em derivada da definição.
por paulohenrique_ » Dom Dez 09, 2012 16:05
- 1 Respostas
- 1937 Exibições
- Última mensagem por young_jedi

Dom Dez 09, 2012 18:12
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em derivada
por luiz3107 » Seg Ago 23, 2010 02:50
- 2 Respostas
- 1925 Exibições
- Última mensagem por luiz3107

Seg Ago 23, 2010 15:15
Cálculo: Limites, Derivadas e Integrais
-
- Derivada duvida
por Isabela Sa » Ter Jul 12, 2011 11:46
- 5 Respostas
- 2737 Exibições
- Última mensagem por LuizAquino

Qua Jul 13, 2011 10:07
Cálculo: Limites, Derivadas e Integrais
-
- Duvida Derivada.
por Bio10ct » Qua Abr 18, 2012 09:17
- 1 Respostas
- 1061 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 11:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 =
= ![\left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right] \left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right]](/latexrender/pictures/4da6df81b35355fd2435511458c74605.png) =
=


 =
= ![\left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right] \left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right]](/latexrender/pictures/4da6df81b35355fd2435511458c74605.png) =
=

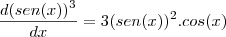
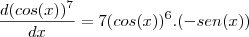

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.