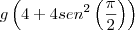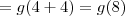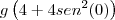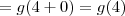Seja
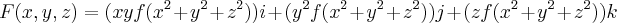 ,
,onde f:
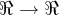 é uma função diferenciável. Seja g:
é uma função diferenciável. Seja g: 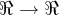 uma
umaantiderivada de f, tal que g(8) = 10 e g(4) = 2. Calcule
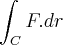 , onde C é a parte da interseção da superfície cilíndrica x² + y² = 4 com o plano z = y, contida no primeiro octante, orientada no sentido antihorário quando vista de cima.
, onde C é a parte da interseção da superfície cilíndrica x² + y² = 4 com o plano z = y, contida no primeiro octante, orientada no sentido antihorário quando vista de cima.Obs.: é uma função vetorial.


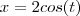
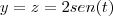
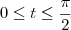
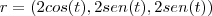
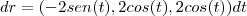

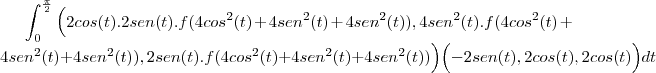
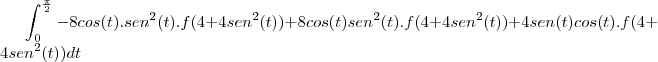
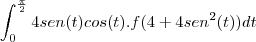
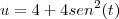
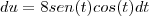
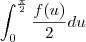
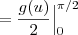
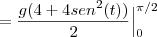
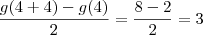
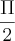 ? Não entendi essa passagem.
? Não entendi essa passagem.