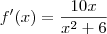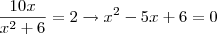por claudia_ » Dom Out 25, 2009 15:04
por claudia_ » Dom Out 25, 2009 15:04
Tenho um problema ao qual nao tenho a certeza sobre a resoluçao , se alguem me pudesse ajudar agradecia ..
O problema e´o seguinte :
Considere a função de variável real definida por f(x)= 5*log(x^2 + 6) . Determine os pontos onde a recta tangente ao gráfico da função f é perpendicular à recta de equação 2y+x=1 .
Agradeço qualquer ajuda ..
-
claudia_
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Out 25, 2009 14:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: CC
- Andamento: cursando
 por Marcampucio » Dom Out 25, 2009 21:05
por Marcampucio » Dom Out 25, 2009 21:05
Por favor esclareça:
1-
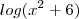
é o logarítmo em base

ou neperiano?
2- o sinal de
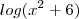
é mesmo
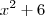
ou seria

?
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por claudia_ » Seg Out 26, 2009 14:27
por claudia_ » Seg Out 26, 2009 14:27
o logaritmo e' neperiano e a função é log na base e de (x^2+6) .
-
claudia_
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Out 25, 2009 14:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: CC
- Andamento: cursando
 por Marcampucio » Seg Out 26, 2009 14:41
por Marcampucio » Seg Out 26, 2009 14:41
A reta sobre a qual as tangentes devem ser perpendiculares é
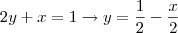
e portanto o coeficiente angular das perpendiculares deverá ser

.
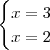
A derivada no ponto fornece o coeficiente angular da tangente, então queremos os valores de

para os quais
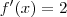
.
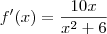
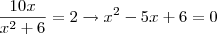
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11058 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida PA
por Cleyson007 » Dom Jun 01, 2008 01:01
- 2 Respostas
- 10770 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Progressões
-
- Dúvida
por miguelbaptista » Sex Jan 09, 2009 03:29
- 8 Respostas
- 12554 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:13
Logaritmos
-
- dúvida
por gdarius » Dom Ago 16, 2009 00:09
- 1 Respostas
- 3159 Exibições
- Última mensagem por Felipe Schucman

Dom Ago 16, 2009 02:35
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida!!
por GABRIELA » Qui Set 17, 2009 18:19
- 5 Respostas
- 5739 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


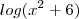 é o logarítmo em base
é o logarítmo em base  ou neperiano?
ou neperiano?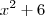 ou seria
ou seria  ?
?
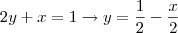 e portanto o coeficiente angular das perpendiculares deverá ser
e portanto o coeficiente angular das perpendiculares deverá ser  .
. para os quais
para os quais 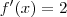 .
.