Então cara, essa questão é simples de resolver, mas como você estava resolvendo exercícios só de trigonometria, talvez não tenha percebido.
Isso é simplesmente uma soma de P.G. infinita cuja razão vale Sen²a.
Temos essa soma:
Sen^2 a + Sen^4 a + ... + Sen^2n a
Ele me dá uma restrição de que K não pode ser 90, 270 ou qualquer outro ângulo côngruo a esses. Claro, por que Sen² 90, ou Sen²270 daria 1, e a soma seria uma soma infinita de termos iguais, no caso, 1.
Mas isso não vem ao caso, é só uma restrição, nem precisa notar isso, ele só diz isso pra que o exercício se torne possível.
Se você separar os termos dessa soma você vai ter:
a1 = Sen^2 a
a2 = Sen^4 a
a3 = Sen^6 a
an = Sen^2n a
Aí você tem que perceber que se trata de uma PG, cuja a razão é Sen^2 a, claro, pois de a1 para a2, basta multiplicarmos a1 por Sen^2 a e teremos o resultado de a2 e assim sucessivamente.
Pronto, a questão acabou aí.
Como eu disse, isso é uma soma de PG Infinita e a fórmula é: S = a1/(1-q)
Você tem a1 e descobriu que q = Sen^2 a
S = Sen^2 a/(1 - Sen^2 a)
Só que pela relação fundamental da trigonometria a gente tem: Sen^2 a + Cos^2 a = 1, e isolando o Cos^2 a, temos: Cos^2 a = 1 - Sen^2a
Então: S = Sen^2 a /Cos^2 a = tg^2 a
Espero ter ajudado!

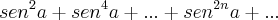 onde
onde 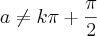 e k pertence aos inteiros, é:
e k pertence aos inteiros, é: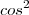 a
a a
a a
a
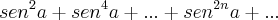 onde
onde 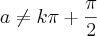 e k pertence aos inteiros, é:
e k pertence aos inteiros, é: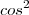 a
a a
a a
a


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)