 por Victor Gabriel » Qui Abr 18, 2013 13:24
por Victor Gabriel » Qui Abr 18, 2013 13:24
Suponha f integrável em
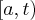
,para todo

. Prove que se
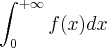
também é convergente. ( Sugestão:use que
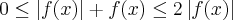
e que

.
Tem alguém que pode mim ajuda na resolução desta questão, pois não sei nem por onde começa!
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por Victor Gabriel » Dom Abr 21, 2013 12:03
por Victor Gabriel » Dom Abr 21, 2013 12:03
Victor Gabriel escreveu:Suponha f integrável em
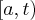
,para todo

. Prove que se
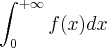
também é convergente. ( Sugestão:use que
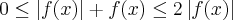
e que

.
Tem alguém que pode mim ajuda na resolução desta questão, pois não sei nem por onde começa!
e pessoal tem como alguém mim ajudar nesta questão?
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Converge ou diverge a sequencia
por Buda » Seg Out 24, 2011 21:28
- 11 Respostas
- 17099 Exibições
- Última mensagem por LuizAquino

Qua Nov 02, 2011 11:15
Sequências
-
- Série converge ou diverge
por Crist » Seg Fev 25, 2013 21:51
- 2 Respostas
- 2373 Exibições
- Última mensagem por Crist

Sáb Mar 02, 2013 10:16
Sequências
-
- Integral: converge
por Victor Gabriel » Seg Abr 29, 2013 14:57
- 0 Respostas
- 880 Exibições
- Última mensagem por Victor Gabriel

Seg Abr 29, 2013 14:57
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4623 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4591 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
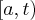 ,para todo
,para todo  . Prove que se
. Prove que se 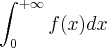 também é convergente. ( Sugestão:use que
também é convergente. ( Sugestão:use que 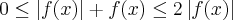 e que
e que  .
.
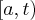 ,para todo
,para todo  . Prove que se
. Prove que se 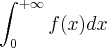 também é convergente. ( Sugestão:use que
também é convergente. ( Sugestão:use que 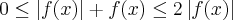 e que
e que  .
.
,para todo
. Prove que se
também é convergente. ( Sugestão:use que
e que
.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)