 por dehcalegari » Ter Abr 16, 2013 15:19
por dehcalegari » Ter Abr 16, 2013 15:19
Calcule
![\lim_{0} \frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} \lim_{0} \frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x}](/latexrender/pictures/edda9baa01ce4d210e74406947d1ae65.png)
Minha resolução que bateu com o gabarito, mas não sei se está correto o desenvolvimento
Substituição:
![\sqrt[]{1+x}=p |||| \sqrt[]{x}=p-1 |||| x=p+1 \sqrt[]{1+x}=p |||| \sqrt[]{x}=p-1 |||| x=p+1](/latexrender/pictures/0a9a3947693293697f20b900f094363c.png)
Logo
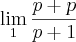
= 2/2 = 1.
Eita, tá errado esse raciocínio, só pode.
-
dehcalegari
- Usuário Parceiro

-
- Mensagens: 85
- Registrado em: Qui Abr 04, 2013 09:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por DanielFerreira » Ter Abr 16, 2013 15:24
por DanielFerreira » Ter Abr 16, 2013 15:24
Infelizmente, sim. Está errado!!
Não podes eliminar o 1 da raiz, pois há uma soma.
O correto seria:
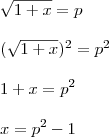
Tente racionalizar o numerador!
Consegue?!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Ter Abr 16, 2013 15:47
por DanielFerreira » Ter Abr 16, 2013 15:47
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por dehcalegari » Ter Abr 16, 2013 15:54
por dehcalegari » Ter Abr 16, 2013 15:54
Ok... Aprendendo...
Nunca tirar um número de um raiz onde há uma soma.
Ok, racionalizando, consegui resolver sim.
Valeu.
-
dehcalegari
- Usuário Parceiro

-
- Mensagens: 85
- Registrado em: Qui Abr 04, 2013 09:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por DanielFerreira » Ter Abr 16, 2013 16:39
por DanielFerreira » Ter Abr 16, 2013 16:39
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- CONFERIR SE ESTÁ CERTO
por gabimucedola » Sex Abr 02, 2010 18:11
- 1 Respostas
- 1566 Exibições
- Última mensagem por davi_11

Sáb Abr 03, 2010 13:37
Matemática Financeira
-
- [Equação Linear] so pra conferir
por dolmian » Dom Jan 13, 2013 20:34
- 2 Respostas
- 1188 Exibições
- Última mensagem por dolmian

Seg Jan 14, 2013 10:49
Álgebra Elementar
-
- Resolução de limites
por Ana Saldanha » Sáb Mai 24, 2014 16:39
- 1 Respostas
- 1068 Exibições
- Última mensagem por e8group

Sáb Mai 24, 2014 17:44
Cálculo: Limites, Derivadas e Integrais
-
- Exercico Limites ajuda na resolução
por pereirva » Seg Abr 20, 2009 19:12
- 4 Respostas
- 4051 Exibições
- Última mensagem por pereirva

Ter Abr 21, 2009 14:19
Cálculo: Limites, Derivadas e Integrais
-
- Estrategias para resoluçao de limites
por Claudin » Dom Mai 15, 2011 14:13
- 7 Respostas
- 4043 Exibições
- Última mensagem por Claudin

Seg Mai 16, 2011 01:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{0} \frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} \lim_{0} \frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x}](/latexrender/pictures/edda9baa01ce4d210e74406947d1ae65.png)
![\sqrt[]{1+x}=p |||| \sqrt[]{x}=p-1 |||| x=p+1 \sqrt[]{1+x}=p |||| \sqrt[]{x}=p-1 |||| x=p+1](/latexrender/pictures/0a9a3947693293697f20b900f094363c.png)
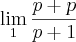 = 2/2 = 1.
= 2/2 = 1.
![\lim_{0} \frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x} \lim_{0} \frac{\sqrt[]{1+x}-\sqrt[]{1-x}}{x}](/latexrender/pictures/edda9baa01ce4d210e74406947d1ae65.png)
![\sqrt[]{1+x}=p |||| \sqrt[]{x}=p-1 |||| x=p+1 \sqrt[]{1+x}=p |||| \sqrt[]{x}=p-1 |||| x=p+1](/latexrender/pictures/0a9a3947693293697f20b900f094363c.png)
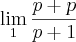 = 2/2 = 1.
= 2/2 = 1.
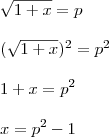






 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.