 por Tay » Qua Abr 10, 2013 22:02
por Tay » Qua Abr 10, 2013 22:02
Olá,
Nem a categoria que o exercício se enquadra eu sei. Mas é esse:
Na igualdade 2x-2 = 1.300, x é um número real compreendido
entre
(A) 8 e 9
(B) 9 e 10
(C) 10 e 11
(D) 11 e 12
(E) 12 e 13
Como calcular esse tipo de exercício, alguém pode me ajudar?
Obrigada.
A palavra é o meu domínio sobre o mundo.
-

Tay
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Seg Mar 18, 2013 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Letras
- Andamento: formado
 por Cleyson007 » Qua Abr 10, 2013 23:20
por Cleyson007 » Qua Abr 10, 2013 23:20
Boa noite
Tay!
Acredito que você escreveu errado..
2^x-2 = 1300 (Dois elevado a x menos dois é igual a mil e trezentos)
Resolvendo: 2^x / 2^2 = 1300 --> 2^x = 2^2 . 1300 --> 2^x = 4. 1300 --> 2^x = 5200
Repare que 2^12 = 4096 e 2^13 = 8192. Logo, 4092 < 5200 <8192, ou seja, 12< x < 13.
Se eu não estiver errado, a resposta é a alternativa "e". Possui o gabarito?
Bons estudos

Atenciosamente,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Tay » Sex Abr 12, 2013 22:19
por Tay » Sex Abr 12, 2013 22:19
Boa noite
Cleyson007,
Sim, eu escrevi errado mesmo (copie e colei e apareceu errado aqui).
A resposta é E.
Você pode, por favor, colocar daquele jeito que você escreve (editor de formas)? Não estou conseguindo acompanhar certinho.

Muitooo Obrigada!
A palavra é o meu domínio sobre o mundo.
-

Tay
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Seg Mar 18, 2013 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Letras
- Andamento: formado
 por Cleyson007 » Sex Abr 12, 2013 23:47
por Cleyson007 » Sex Abr 12, 2013 23:47
Boa noite
Tay!
Claro que sim


Resolvendo:
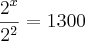
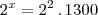
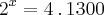
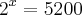
Repare que
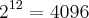
e

. Logo,
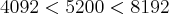
, ou seja,
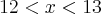
.
Qualquer dúvida estou a disposição

Bons estudos.
Cleyson007Editado pela última vez por
Cleyson007 em Dom Abr 14, 2013 12:55, em um total de 1 vez.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Tay » Sáb Abr 13, 2013 20:40
por Tay » Sáb Abr 13, 2013 20:40
Boa Noite Cleyson007,
Obrigadaa!
Diria que apenas isso resumi tudo:



A palavra é o meu domínio sobre o mundo.
-

Tay
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Seg Mar 18, 2013 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Letras
- Andamento: formado
 por Cleyson007 » Dom Abr 14, 2013 12:58
por Cleyson007 » Dom Abr 14, 2013 12:58
Bom dia Tay!
Por nada, qualquer dúvida estou a disposição

A explicação ficou clara?
A expressão foi de espanto? rsrs
Tenha um bom Domingo!
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Tay » Seg Abr 15, 2013 20:53
por Tay » Seg Abr 15, 2013 20:53
Boa noite Cleison007,
Obrigada e ficou clara sim!

O espanto é porque é difícil para uma leiga como eu. rsrs
A palavra é o meu domínio sobre o mundo.
-

Tay
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Seg Mar 18, 2013 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Letras
- Andamento: formado
 por Cleyson007 » Ter Abr 16, 2013 07:47
por Cleyson007 » Ter Abr 16, 2013 07:47
Ah sim, tudo bem..

Qualquer coisa estou a disposição

Bons estudos!
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão cesgranrio
por Tay » Sáb Mar 30, 2013 17:33
- 19 Respostas
- 13365 Exibições
- Última mensagem por Tay

Sex Abr 12, 2013 22:22
Matemática Financeira
-
- Questão Cesgranrio - Dúvida
por Tay » Seg Mar 18, 2013 13:46
- 2 Respostas
- 2484 Exibições
- Última mensagem por Tay

Sex Mar 22, 2013 21:04
Lógica
-
- Preciso de ajuda com essa questão da Fundação Cesgranrio
por Jesicaa » Qui Mar 12, 2015 11:46
- 2 Respostas
- 3156 Exibições
- Última mensagem por Jesicaa

Dom Mar 15, 2015 00:06
Sistemas de Equações
-
- cesgranrio
por Maria Livia » Sex Set 06, 2013 10:15
- 0 Respostas
- 1518 Exibições
- Última mensagem por Maria Livia

Sex Set 06, 2013 10:15
Trigonometria
-
- Cesgranrio - Juros
por Tay » Qui Jan 30, 2014 14:05
- 3 Respostas
- 5822 Exibições
- Última mensagem por Tay

Sex Fev 07, 2014 12:12
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 Muitooo Obrigada!
Muitooo Obrigada!

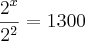
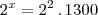
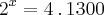
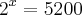
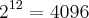 e
e  . Logo,
. Logo, 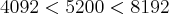 , ou seja,
, ou seja, 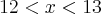 .
.
