 por Jhennyfer » Ter Abr 09, 2013 14:03
por Jhennyfer » Ter Abr 09, 2013 14:03
Dois ângulos complementares A e B, sendo A < B, têm medidas na razão de 13 para17. consequentemente, a razão da medida do suplemento do ângulo A para o suplemento do ângulo B vale:
a) 43/47 b)17/13 c)13/17 d)119/48 e)47/43
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Ter Abr 09, 2013 19:43
por e8group » Ter Abr 09, 2013 19:43
Pelo encunciado temos que :
(a)
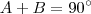
(b)
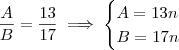
para algum
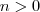
.
(c) Tal número

é 3 ,pois (a)+(b)
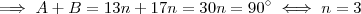
.
(d) O suplemento dos ângulos

e

são ,respectivamente ,
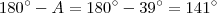
e
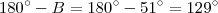
(e) Conclusão :
... complete você .
Tente concluir .
Deve encontar 47/43 .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Ter Abr 09, 2013 20:25
por Jhennyfer » Ter Abr 09, 2013 20:25
Consegui compreender...
Me confundi na parte inicial, por isso não consegui desenvolver o calculo...
Neste outro caso... uso a mesma linha de raciocinio? Estou resolvendo, e está dando uma conta enorme.
(CEFET-CE) Dois ângulos são suplementares. Os 2/3 do maior excedem os 3/4 do menor em 69º. Determine os ângulos:
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Ter Abr 09, 2013 20:50
por e8group » Ter Abr 09, 2013 20:50
OK.Só uma observação ,post uma única dúvida por tópico ,certo ?
Então , vamos impor que

e

são ângulos com
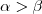
e
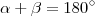
. Pelo enunciado "... Os 2/3 do maior excedem os 3/4 do menor em 69º ..." ,nesta parte diz que
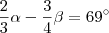
.
Em resumo temos um sistema de duas equações para duas incógnitas ,precisamos encontrar

e

tais que satisfaçam cada equação do sistema
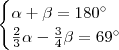
.
Consegue concluir ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Qui Abr 11, 2013 00:52
por Jhennyfer » Qui Abr 11, 2013 00:52
Ok, eu sei dessa regra e esqueci, desculpa (rs...)
Enfim... Na minha solução 36º e 144º... correto?
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Abr 11, 2013 12:35
por e8group » Qui Abr 11, 2013 12:35
Se
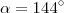
e
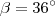
satisfazerem as duas equações ,então sua resposta está correta .
Verificando :
(1)
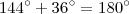
(OK !!)
(2)
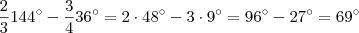
(OK!!) .
Está correto a sua resposta .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



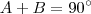
 para algum
para algum 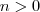 .
.  é 3 ,pois (a)+(b)
é 3 ,pois (a)+(b) 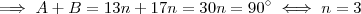 .
. e
e  são ,respectivamente ,
são ,respectivamente , 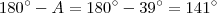 e
e 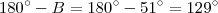


 e
e  são ângulos com
são ângulos com 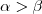 e
e 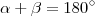 . Pelo enunciado "... Os 2/3 do maior excedem os 3/4 do menor em 69º ..." ,nesta parte diz que
. Pelo enunciado "... Os 2/3 do maior excedem os 3/4 do menor em 69º ..." ,nesta parte diz que 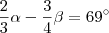 .
.  e
e  tais que satisfaçam cada equação do sistema
tais que satisfaçam cada equação do sistema 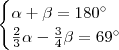 .
.

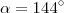 e
e 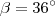 satisfazerem as duas equações ,então sua resposta está correta .
satisfazerem as duas equações ,então sua resposta está correta . 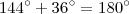 (OK !!)
(OK !!)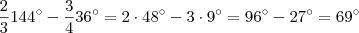 (OK!!) .
(OK!!) .


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.