 por Lana Brasil » Ter Abr 09, 2013 16:45
por Lana Brasil » Ter Abr 09, 2013 16:45
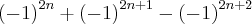
Qual a forma mais fácil de resolver, por favor? Não consegui.
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Ter Abr 09, 2013 20:00
por e8group » Ter Abr 09, 2013 20:00
Temos :
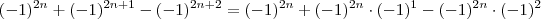
Ou ainda ,
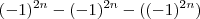
.
Observações :
Para qualquer que seja

real ,
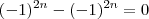
;além disto ,caso

seja inteiro temos que
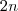
é par , logo
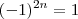
para todo n inteiro .
Portanto ,

.
Cabe a analisar quem é "n" ,dependendo de quem o for ,não representará um número real , tome
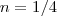
por exemplo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Ter Abr 09, 2013 20:01
por e8group » Ter Abr 09, 2013 20:01
Na verdade ,
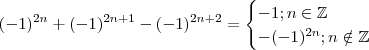
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lana Brasil » Ter Abr 09, 2013 20:22
por Lana Brasil » Ter Abr 09, 2013 20:22
santhiago escreveu:Temos :
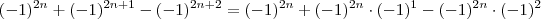
Ou ainda ,
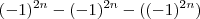
.
Observações :
Para qualquer que seja

real ,
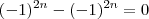
;além disto ,caso

seja inteiro temos que
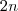
é par , logo
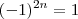
para todo n inteiro .
Portanto ,

.
Cabe a analisar quem é "n" ,dependendo de quem o for ,não representará um número real , tome
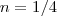
por exemplo .
Muito obrigada pela ajuda.
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Potência com incógnita no expoente
por Rayane01 » Qua Dez 21, 2016 19:12
- 1 Respostas
- 3227 Exibições
- Última mensagem por petras

Qui Dez 22, 2016 22:44
Equações
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3690 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3779 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
-
- [Potencia] soma de potencia com letras
por carla villela » Qui Mar 01, 2012 21:04
- 8 Respostas
- 8638 Exibições
- Última mensagem por carla villela

Qui Mar 01, 2012 22:18
Sistemas de Equações
-
- Incógnita de logaritmo
por usuariomatematica » Ter Mai 31, 2011 09:18
- 0 Respostas
- 1689 Exibições
- Última mensagem por usuariomatematica

Ter Mai 31, 2011 09:18
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
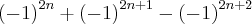

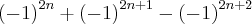

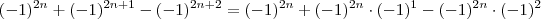
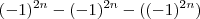 .
.  real ,
real , 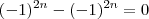 ;além disto ,caso
;além disto ,caso  seja inteiro temos que
seja inteiro temos que 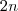 é par , logo
é par , logo 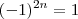 para todo n inteiro .
para todo n inteiro .  .
.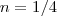 por exemplo .
por exemplo .
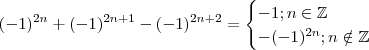

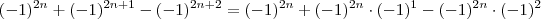
.
real ,
;além disto ,caso
seja inteiro temos que
é par , logo
para todo n inteiro .
.
por exemplo .


 .
.



