 por _bruno94 » Dom Abr 07, 2013 22:19
por _bruno94 » Dom Abr 07, 2013 22:19
Qual o valor de x na equação
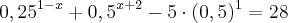
?
Pessoal, esta é uma questão do meu trabalho e eu não estou conseguindo achar uma resposta pra ela. Todas minhas tentativas resultam em contas impossíveis para alguém do ensino médio fazer. Eu acho que há algum erro de digitação por parte do professor.
Façam, por favor, e vejam se concordam comigo.
Desde já, obrigado.
-
_bruno94
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Abr 07, 2013 22:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Russman » Dom Abr 07, 2013 22:52
por Russman » Dom Abr 07, 2013 22:52
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por _bruno94 » Seg Abr 08, 2013 18:25
por _bruno94 » Seg Abr 08, 2013 18:25
Ok, entendi.
Substituindo
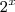
por

vamos ter:
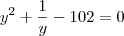
Certo?
Como, a partir disto, você chegou em

?
Resolvendo esta equação, o delta não dá um quadrado perfeito. Assim não consigo resolver a equação exponencial. Eu esperava como resposta desta equação de 2º grau um número do tipo
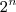
(n inteiro).
Eu acho que esta equação está errada.
Obrigado.
-
_bruno94
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Abr 07, 2013 22:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Russman » Seg Abr 08, 2013 21:20
por Russman » Seg Abr 08, 2013 21:20
Você tem razão. Me enganei no desenvolvimento da equação. O correto é
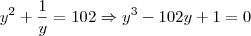
e essa equação não tem raízes reais. ;/
Aliás, a equação original em x também não tem solução real.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por armando » Ter Abr 09, 2013 19:00
por armando » Ter Abr 09, 2013 19:00
Oi _Bruno94 !
Eu creio que o Russman se enganou logo no início da resolução.
Qual o valor de x na equação
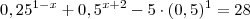
?
Repare que você no enunciado digitou:
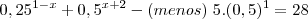
e o Russman após transformar os decimais em potências escreveu:
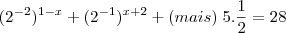
Passando os
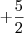
para juto dos
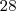
para a direita do sinal de igual, estes passam a:

o que dá:
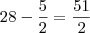
O correcto será :
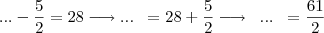
Eu resolvi a equação numa calculadora TI nspire CAS, e esta deu como resultado:
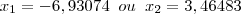
O que quer dizer que ela admite 2 raízes reais.
Creio que a sua dificuldade possa resultar dessa situação.
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Ter Abr 09, 2013 21:44
por DanielFerreira » Ter Abr 09, 2013 21:44
 Bruno
Bruno,
concordo! Provavelmente tenha algum erro na equação. Os números são...
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com equação exponencial...
por Cristiano87 » Dom Nov 07, 2010 22:39
- 1 Respostas
- 1252 Exibições
- Última mensagem por Elcioschin

Dom Nov 07, 2010 22:43
Sistemas de Equações
-
- Alguem me ajuda nessa equação exponencial
por raphael11234 » Qua Jun 08, 2016 00:07
- 1 Respostas
- 4727 Exibições
- Última mensagem por Cleyson007

Qua Jun 08, 2016 15:20
Equações
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1625 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2838 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2828 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
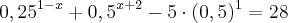 ?
?



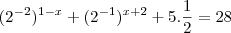
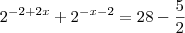
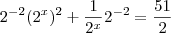
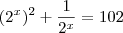
 , de forma que
, de forma que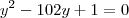
 possíveis.
possíveis.
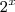 por
por  vamos ter:
vamos ter: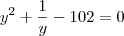
 ?
?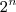 (n inteiro).
(n inteiro).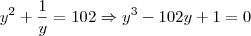
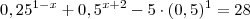 ?
?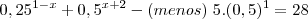
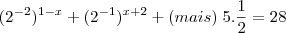
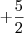 para juto dos
para juto dos 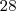 para a direita do sinal de igual, estes passam a:
para a direita do sinal de igual, estes passam a:  o que dá:
o que dá: 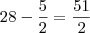
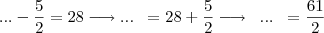
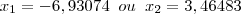

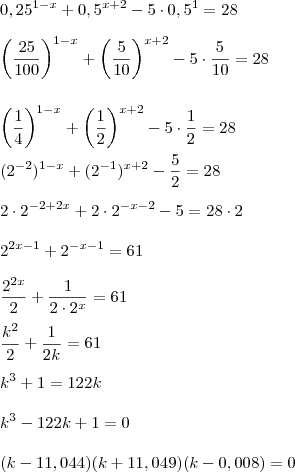



 , avisa que eu resolvo.
, avisa que eu resolvo.

