 por marcosmuscul » Qui Abr 04, 2013 17:34
por marcosmuscul » Qui Abr 04, 2013 17:34

minha resolução:
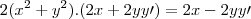
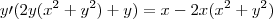
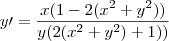
para achar reta horizontal:
basta que a expressão do numerador de 0
para achar reta vertical:
basta que a expressão do denominador de 0
não consigo passar disto pois em ambos os casos chego a uma equação de círculo para o primeiro e uma parecida com a de circulo para o segundo.
o ponto (0,0) sei que é de inflexão.
me ajudem, please.
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por Russman » Qui Abr 04, 2013 18:19
por Russman » Qui Abr 04, 2013 18:19
marcosmuscul escreveu:para achar reta horizontal:
basta que a expressão do numerador de 0
para achar reta vertical:
basta que a expressão do denominador de 0
O seu raciocínio esta correto. Porém, não esqueça que, você deve garantir também no 1° caso que o denominador não se anule. Se isto acontecer você terá o quociente

que pode ser diferente de

. No 2° caso você deve garantir que o numerador não se anule pelo mesmo motivo.
Acrescente estas duas novas condições e eu acredito que você será capaz de resolver completamente o problema.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Assintota vertical e horizontal
por Zercamga » Seg Set 17, 2012 12:30
- 6 Respostas
- 10190 Exibições
- Última mensagem por Zercamga

Ter Set 18, 2012 17:32
Cálculo: Limites, Derivadas e Integrais
-
- Pontos onde a reta Tangente é vertical:
por gabrielb44 » Sáb Nov 18, 2017 20:35
- 0 Respostas
- 1800 Exibições
- Última mensagem por gabrielb44

Sáb Nov 18, 2017 20:35
Cálculo: Limites, Derivadas e Integrais
-
- Não consigo achar o limite
por CrazzyVi » Sáb Nov 14, 2009 13:34
- 2 Respostas
- 2506 Exibições
- Última mensagem por CrazzyVi

Qui Dez 10, 2009 14:28
Cálculo: Limites, Derivadas e Integrais
-
- Não consigo achar o determinante
por IsabelRangell » Qui Abr 08, 2010 17:08
- 1 Respostas
- 2508 Exibições
- Última mensagem por MarceloFantini

Qui Abr 08, 2010 19:55
Matrizes e Determinantes
-
- Nao consigo achar a forma reduzida da matriz..
por PeIdInHu » Seg Jun 14, 2010 23:07
- 1 Respostas
- 2580 Exibições
- Última mensagem por PeIdInHu

Seg Jun 14, 2010 23:55
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

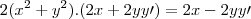
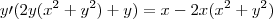
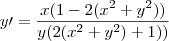


 que pode ser diferente de
que pode ser diferente de  . No 2° caso você deve garantir que o numerador não se anule pelo mesmo motivo.
. No 2° caso você deve garantir que o numerador não se anule pelo mesmo motivo. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.