 por Bellamv » Ter Mar 26, 2013 01:55
por Bellamv » Ter Mar 26, 2013 01:55
Na expressão
3.log x + log (2y) -1 pedem pra reduzir a um único log
Minha dúvida é no (-1), eu tenho q transformar em log? n sei oq fazer xP
se fosse sem o (-1) daria
log(x³.2.y)A resposta ta como
log((x³.2.y)/b)ps: todos os logs estão na base "b"Me expliquem como chegar nisso plis..
Desde já agradeço

-
Bellamv
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Out 27, 2012 00:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Ter Mar 26, 2013 02:27
por Russman » Ter Mar 26, 2013 02:27
Lembre-se que
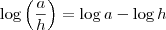
.
Se a base do logaritmo é

, então
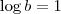
, certo? Assim,
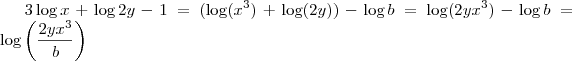
.
Entende?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Bellamv » Ter Mai 14, 2013 03:22
por Bellamv » Ter Mai 14, 2013 03:22
Nossa muito obrigada, agora entendi... era simples, só n pensei nisso hehehe
-
Bellamv
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Out 27, 2012 00:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


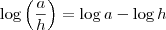 .
. , então
, então 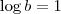 , certo? Assim,
, certo? Assim, 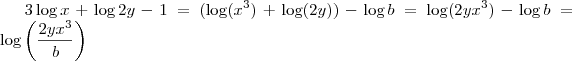 .
.
