 por klueger » Qui Mar 21, 2013 10:19
por klueger » Qui Mar 21, 2013 10:19
Não tenho noção dessa...
Para construir telhas corrugadas usam-se folhas planas de metal com comprimento
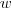
.
Ao processar estas folhas de metal o perfil da telha tem a forma de uma função senoidal com 60cm de comprimento e 4 cm de espessura.
A função senoidal é dada por

a) Qual a integral que dará o comprimento de arco?
b) Qual o comprimento da curva dado por

, sendo

-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Qui Mar 21, 2013 12:26
por Russman » Qui Mar 21, 2013 12:26
Dada uma curva
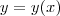
, o seu comprimento de

até

é dado por

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por klueger » Qui Mar 21, 2013 12:36
por klueger » Qui Mar 21, 2013 12:36
Não esclareceu tudo ainda :/
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Qui Mar 21, 2013 12:43
por Russman » Qui Mar 21, 2013 12:43
Comece derivando a função e elevando essa derivada ao quadrado, como manda a fórmula.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por klueger » Qui Mar 21, 2013 12:47
por klueger » Qui Mar 21, 2013 12:47
Obrigado. Tentarei fazer aqui

Quanto a letra A, a integral que forma o arco, seria deduzida como?
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Qui Mar 21, 2013 12:54
por Russman » Qui Mar 21, 2013 12:54
É essa integral que eu te escrevi.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- comprimento do arco
por liviabgomes » Seg Mai 30, 2011 16:11
- 10 Respostas
- 6244 Exibições
- Última mensagem por liviabgomes

Qua Jun 01, 2011 15:03
Cálculo: Limites, Derivadas e Integrais
-
- comprimento de arco
por manuoliveira » Ter Out 23, 2012 19:43
- 0 Respostas
- 1313 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 19:43
Cálculo: Limites, Derivadas e Integrais
-
- comprimento do arco
por VenomForm » Seg Mai 20, 2013 13:29
- 0 Respostas
- 1248 Exibições
- Última mensagem por VenomForm

Seg Mai 20, 2013 13:29
Cálculo: Limites, Derivadas e Integrais
-
- Calculo do comprimento do arco.
por brunojorge29 » Seg Abr 23, 2012 11:21
- 3 Respostas
- 2965 Exibições
- Última mensagem por Russman

Seg Abr 23, 2012 22:32
Cálculo: Limites, Derivadas e Integrais
-
- Comprimento do arco!! Urgente!!
por manuoliveira » Ter Out 23, 2012 20:34
- 4 Respostas
- 3498 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 21:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
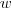 .
. 
 , sendo
, sendo 


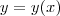 , o seu comprimento de
, o seu comprimento de  até
até  é dado por
é dado por .
.
