 por Douglas16 » Dom Mar 10, 2013 17:38
por Douglas16 » Dom Mar 10, 2013 17:38
Neste link está a prova:
http://pt.wikipedia.org/wiki/Prova_de_irracionalidade_do_n%C3%BAmero_de_EulerMas não sei como na penúltima equação a expressão: fatorial de b, sobre, o fatorial de n, é igual a:

E também como provar a afirmação: "E o resultado segue, pois como é fácil ver 2<e<3"; não encontro a prova!!!???
O resto entendi, ok?
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Mar 10, 2013 18:50
por e8group » Dom Mar 10, 2013 18:50
Boa tarde .Observe que por hipótese
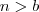
e ambos são naturais .Certo ?
Desta forma, existe algum

natural tal que

(Não é verdade ? )
Assim ,

.
Substituindo-se

, segue que
![n! = (b+[n -b])\cdot (b+[n -b] -1)\cdot (b+[n -b]-2)\cdot (b+[n -b]-3) \cdots (b +1) ) \cdot b! n! = (b+[n -b])\cdot (b+[n -b] -1)\cdot (b+[n -b]-2)\cdot (b+[n -b]-3) \cdots (b +1) ) \cdot b!](/latexrender/pictures/21393c327fa4a29315160b57ca55c2d7.png)
que simplificando ficamos apenas com ,

.
Logo ,

.
Qualquer dúvida só postar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Mar 10, 2013 20:20
por e8group » Dom Mar 10, 2013 20:20
Boa noite ,eu fiz este exercício há algum tempo atrás , vou disponibilizar com a intenção de ajudar .
Seja

(é irracional)
Demostração :
(1) Vamos supor
por absurdo que existem

Multiplicando-se

por

,temos

.
Mas ,

,então :
(*)

.
(2)Vale destacar que os membros à esquerda da igualdade acima são naturais , logo ,

e

também são naturais .
Além disso , a igualdade (* )pode ser escrita como ,
 (3)
(3) Se mostrarmos que

não é natural ,está concluída a prova .
De fato este número não o é . Pois ,

=

Ou seja ,
 (4)
(4) Conclusão (2) + (3) contradiz (1) .

.
Qualquer dúvida estou a disposição ,ficaria muito grato se alguém corrigisse a demostração acima caso notarem algum erro .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Número de Euler
por Aliocha Karamazov » Sex Out 28, 2011 20:16
- 2 Respostas
- 4339 Exibições
- Última mensagem por Aliocha Karamazov

Sex Out 28, 2011 22:46
Cálculo: Limites, Derivadas e Integrais
-
- [Limites com número de euler]
por mpborto » Sex Mar 18, 2016 15:29
- 1 Respostas
- 2035 Exibições
- Última mensagem por adauto martins

Sex Mar 18, 2016 17:28
Cálculo: Limites, Derivadas e Integrais
-
- Função de Euler
por Crist » Seg Dez 02, 2013 09:06
- 4 Respostas
- 3750 Exibições
- Última mensagem por Bravim

Sex Dez 06, 2013 03:03
Teoria dos Números
-
- Limite + algarismo de Euler = ????
por EulaCarrara » Seg Abr 19, 2010 21:29
- 5 Respostas
- 4046 Exibições
- Última mensagem por MarceloFantini

Seg Abr 19, 2010 23:11
Cálculo: Limites, Derivadas e Integrais
-
- Geometria - relação de Euler
por marinalcd » Ter Set 04, 2012 19:16
- 1 Respostas
- 1697 Exibições
- Última mensagem por fraol

Dom Set 30, 2012 13:54
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




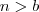 e ambos são naturais .Certo ?
e ambos são naturais .Certo ?  natural tal que
natural tal que  (Não é verdade ? )
(Não é verdade ? ) .
.  , segue que
, segue que ![n! = (b+[n -b])\cdot (b+[n -b] -1)\cdot (b+[n -b]-2)\cdot (b+[n -b]-3) \cdots (b +1) ) \cdot b! n! = (b+[n -b])\cdot (b+[n -b] -1)\cdot (b+[n -b]-2)\cdot (b+[n -b]-3) \cdots (b +1) ) \cdot b!](/latexrender/pictures/21393c327fa4a29315160b57ca55c2d7.png) que simplificando ficamos apenas com ,
que simplificando ficamos apenas com ,  .
.  .
.
 (é irracional)
(é irracional)
 por
por  ,temos
,temos  .
.  ,então :
,então :  .
. e
e  também são naturais .
também são naturais . 
 não é natural ,está concluída a prova .
não é natural ,está concluída a prova . 


 .
. 





