 por AnakinGabriel » Sáb Mar 09, 2013 20:15
por AnakinGabriel » Sáb Mar 09, 2013 20:15
Então pessoal, encontrei essa questão no meu livro e não consegui resolver, eu 'travo' em certos pontos da resolução e não consigo mais avançar.
Resolva o sistema abaixo:
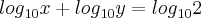
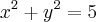
Obrigado.
-
AnakinGabriel
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Mar 09, 2013 19:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico de Informatica
- Andamento: cursando
 por e8group » Sáb Mar 09, 2013 21:46
por e8group » Sáb Mar 09, 2013 21:46
Equações ,
(i)
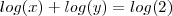
(ii)
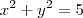
Em (i) por propriedades de logaritmo podemos escrever que
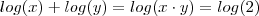
ou ainda que
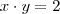
(OK ?)
Em(ii) ,vale destacar que
![x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)] = (x+y)^2 -2xy x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)] = (x+y)^2 -2xy](/latexrender/pictures/78ce3ef875f77cab37c821ad06d844f6.png)
.
Como
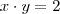
substituindo-se em
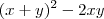
obtemos que
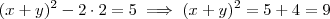
.Extraindo a raiz quadrada em ambos membros
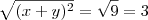
. Visto que a equação (i) estar definida se , e somente se ,
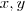
são ambos positivos ,então ficamos apenas com
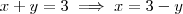
.
Substituindo-se

na equação (i) ou (ii) ,

Basta resolver a equação acima em
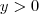
,logo após substitua a solução p/

em
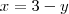
e encontre

.
Tente concluir .
OBS.:
a)
![[2xy +(- 2xy)] = 0 [2xy +(- 2xy)] = 0](/latexrender/pictures/5cf8923927d90c5effb2e75eaed9eb05.png)
não estamos alterando o resultado (elemento neutro adtivo )
b)
![x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)] x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)]](/latexrender/pictures/7006b42c1a815a3688508daf5505bf2c.png)
por associatividade temos que
![x^2 + y^2 + [2xy +(- 2xy)] = (x^2 + y^2 +2xy) -2xy x^2 + y^2 + [2xy +(- 2xy)] = (x^2 + y^2 +2xy) -2xy](/latexrender/pictures/7788148cb259ef1b257cab237c933922.png)
e ainda observando que
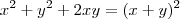
(OK?) , obtemos
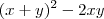
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [puc-pr] logaritmo e sistema
por JKS » Dom Mar 17, 2013 13:32
- 1 Respostas
- 1873 Exibições
- Última mensagem por DanielFerreira

Dom Mar 17, 2013 18:34
Logaritmos
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2577 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1854 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3092 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4499 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
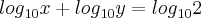
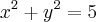

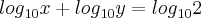
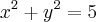

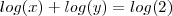
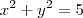
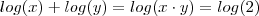 ou ainda que
ou ainda que 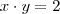 (OK ?)
(OK ?)![x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)] = (x+y)^2 -2xy x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)] = (x+y)^2 -2xy](/latexrender/pictures/78ce3ef875f77cab37c821ad06d844f6.png) .
. 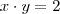 substituindo-se em
substituindo-se em 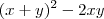 obtemos que
obtemos que 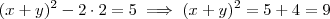 .Extraindo a raiz quadrada em ambos membros
.Extraindo a raiz quadrada em ambos membros 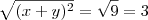 . Visto que a equação (i) estar definida se , e somente se ,
. Visto que a equação (i) estar definida se , e somente se , 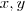 são ambos positivos ,então ficamos apenas com
são ambos positivos ,então ficamos apenas com 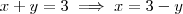 .
.  na equação (i) ou (ii) ,
na equação (i) ou (ii) ,
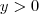 ,logo após substitua a solução p/
,logo após substitua a solução p/  em
em 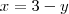 e encontre
e encontre  .
.![[2xy +(- 2xy)] = 0 [2xy +(- 2xy)] = 0](/latexrender/pictures/5cf8923927d90c5effb2e75eaed9eb05.png) não estamos alterando o resultado (elemento neutro adtivo )
não estamos alterando o resultado (elemento neutro adtivo )![x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)] x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)]](/latexrender/pictures/7006b42c1a815a3688508daf5505bf2c.png) por associatividade temos que
por associatividade temos que ![x^2 + y^2 + [2xy +(- 2xy)] = (x^2 + y^2 +2xy) -2xy x^2 + y^2 + [2xy +(- 2xy)] = (x^2 + y^2 +2xy) -2xy](/latexrender/pictures/7788148cb259ef1b257cab237c933922.png) e ainda observando que
e ainda observando que 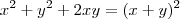 (OK?) , obtemos
(OK?) , obtemos 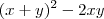 .
.





