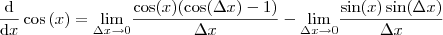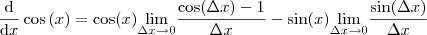por MarlonMO250 » Qui Mar 07, 2013 16:31
por MarlonMO250 » Qui Mar 07, 2013 16:31
Olá, como varias das minhas duvidas ultimamente foram resolvidas por aqui venho denovo pedir ajuda

como logo vou ter uma prova de derivadas decidi começar a estudar logo pra não ir tão mal rs, e me deparei com a seguinte questão:
Mostre, utilizando a definição de derivadas, que: se
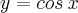
então
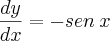
.
no caso como eu devo resolver? simplesmente colocando que:
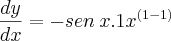
?
-
MarlonMO250
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Fev 03, 2013 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Russman » Qui Mar 07, 2013 20:12
por Russman » Qui Mar 07, 2013 20:12
Você tem de aplicar a definição de derivada.
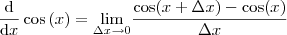
Agora, lembre-se que
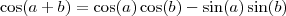
e, portanto
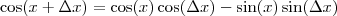
de forma que

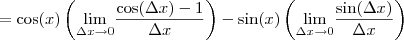
Tudo bem até aqui?
Editado pela última vez por
Russman em Qui Mar 07, 2013 21:04, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MarlonMO250 » Qui Mar 07, 2013 20:43
por MarlonMO250 » Qui Mar 07, 2013 20:43
até aqui:
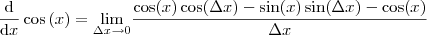
tudo bem.
porem, isso:
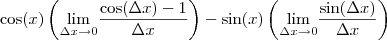
eu não entendi

-
MarlonMO250
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Fev 03, 2013 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Russman » Qui Mar 07, 2013 21:15
por Russman » Qui Mar 07, 2013 21:15
Note que em
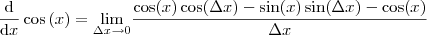
podemos fatorar os termos que apresentam
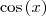
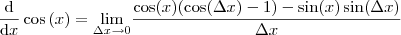
e como o limite opera apenas em

, isto é, todas as funções de

não são afetadas pelo limite e o limite de uma soma é a soma dos limites, podemos fatorá-las.
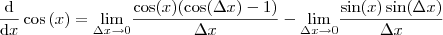
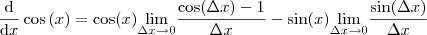
Entende agora?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MarlonMO250 » Sex Mar 08, 2013 11:03
por MarlonMO250 » Sex Mar 08, 2013 11:03
hmmm, saquei

agora outra coisa que fiquei em duvida: "Determine o local (abscissa do ponto) em que a reta tangente à curva y=x², no ponto de abscissa x=5 intercepta o eixo das abscissas (eixo x)."
se puder me ajudar eu agradeço muito

-
MarlonMO250
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Fev 03, 2013 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Russman » Sex Mar 08, 2013 14:13
por Russman » Sex Mar 08, 2013 14:13
Você precisa calcular a inclinação da reta tangente no ponto desejado. Como você deve saber, esta é a derivada da função no ponto. Você já calculou a derivada da função?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1998 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
-
- Calculando derivadas pela definição
por ARCS » Dom Jan 16, 2011 22:57
- 1 Respostas
- 1708 Exibições
- Última mensagem por MarceloFantini

Seg Jan 17, 2011 14:57
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda com a definição formal de limites
por Gustavooguto » Seg Out 13, 2014 23:49
- 1 Respostas
- 2372 Exibições
- Última mensagem por adauto martins

Ter Out 14, 2014 11:19
Funções
-
- Ajuda em derivadas!
por Juninhow » Ter Abr 07, 2015 10:17
- 1 Respostas
- 1009 Exibições
- Última mensagem por Cleyson007

Ter Abr 07, 2015 18:35
Cálculo: Limites, Derivadas e Integrais
-
- [derivadas]Ajuda básica
por MarlonMO250 » Dom Fev 24, 2013 16:37
- 3 Respostas
- 2182 Exibições
- Última mensagem por Russman

Dom Fev 24, 2013 20:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

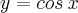 então
então 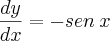 .
.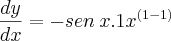 ?
?

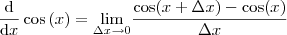
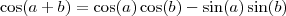
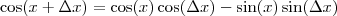

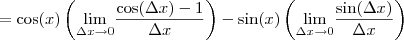

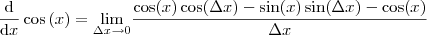 tudo bem.
tudo bem.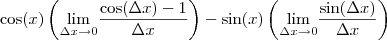 eu não entendi
eu não entendi 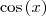
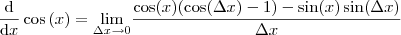
 , isto é, todas as funções de
, isto é, todas as funções de  não são afetadas pelo limite e o limite de uma soma é a soma dos limites, podemos fatorá-las.
não são afetadas pelo limite e o limite de uma soma é a soma dos limites, podemos fatorá-las.