 por Maria Livia » Seg Mar 04, 2013 17:56
por Maria Livia » Seg Mar 04, 2013 17:56
Por que o número natural 2 (elevado a 30) -1 não é primo?
-
Maria Livia
- Usuário Parceiro

-
- Mensagens: 79
- Registrado em: Seg Ago 13, 2012 13:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por marinalcd » Seg Mar 04, 2013 18:19
por marinalcd » Seg Mar 04, 2013 18:19
Não entendi muito bem sua expressão, mas se for isso:
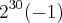
Porque o resultado é um número par e é divisível por 2, 3, 4, 6, 8, .....
Independentemente do sinal.
O sinal só quer dizer que o resultado será negativo. Por exemplo, 3072:3 = -1024.
Mas isso não quer dizer que ele não é múltiplo.
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Maria Livia » Seg Mar 04, 2013 18:36
por Maria Livia » Seg Mar 04, 2013 18:36
Sem o parêntese a expressão é 2 elevado a 30 depois o menos um fora do expoente
-
Maria Livia
- Usuário Parceiro

-
- Mensagens: 79
- Registrado em: Seg Ago 13, 2012 13:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Seg Mar 04, 2013 20:15
por e8group » Seg Mar 04, 2013 20:15
Boa noite parece que sua expressão é esta
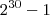
certo ?
Para mostra que
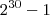
não é primo basta mostra que existe
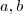
naturais tais que
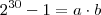
com
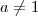
ou
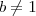
.
OBS.:
Lembre-se ,todo número inteiro não primo é produto de primos.
Note que
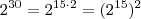
;assim,fazendo
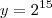
,obtemos :
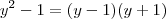
,isto mostra que
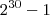
não é primo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- UFPE
por Artur » Qui Abr 08, 2010 17:53
- 1 Respostas
- 3920 Exibições
- Última mensagem por Molina

Qui Abr 08, 2010 18:11
Álgebra Elementar
-
- Ufpe
por Maria Livia » Seg Mar 18, 2013 16:47
- 6 Respostas
- 5564 Exibições
- Última mensagem por timoteo

Ter Mar 19, 2013 12:16
Geometria Espacial
-
- UFPE Lógica
por Abelardo » Qua Mar 09, 2011 20:53
- 10 Respostas
- 13221 Exibições
- Última mensagem por Abelardo

Sáb Mar 12, 2011 03:18
Álgebra Elementar
-
- Probabilidade da UFPE
por [NewtoN] » Qua Dez 21, 2011 12:05
- 2 Respostas
- 4884 Exibições
- Última mensagem por [NewtoN]

Qua Dez 21, 2011 15:47
Estatística
-
- [Análise combinatória] UFPE
por rochadapesada » Seg Abr 08, 2013 20:30
- 2 Respostas
- 4932 Exibições
- Última mensagem por rochadapesada

Ter Abr 09, 2013 03:55
Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



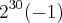


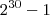 certo ?
certo ? 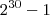 não é primo basta mostra que existe
não é primo basta mostra que existe 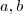 naturais tais que
naturais tais que 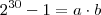 com
com 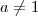 ou
ou 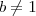 .
.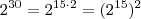 ;assim,fazendo
;assim,fazendo 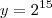 ,obtemos :
,obtemos :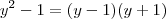 ,isto mostra que
,isto mostra que 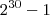 não é primo .
não é primo .


 , avisa que eu resolvo.
, avisa que eu resolvo.

