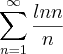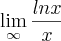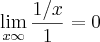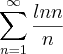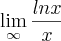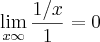por Crist » Seg Fev 25, 2013 21:51
por Crist » Seg Fev 25, 2013 21:51
Preciso determinar se a série converge ou diverge
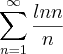
usei a regra de L´Hopital
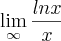
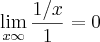
e assim conclui que a série converge, mas estou com dúvida se minha resolução está correta, alguém pode me ajudar?
-
Crist
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qua Out 24, 2012 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Sáb Mar 02, 2013 00:14
por young_jedi » Sáb Mar 02, 2013 00:14
na verdade se o limite tivesse resultado em um valor diferente de zero voce poderia dizer que a serie diverge, mais como ele du zero voce não pode concluir nada, neste caso tente utilizar o teste da integral e comente qualquer duvida.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Crist » Sáb Mar 02, 2013 10:16
por Crist » Sáb Mar 02, 2013 10:16
Obrigada, usei o teste da integral e conclui que a série diverge pois o resultado da integral foi para infinito.

-
Crist
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qua Out 24, 2012 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Converge ou diverge a sequencia
por Buda » Seg Out 24, 2011 21:28
- 11 Respostas
- 17094 Exibições
- Última mensagem por LuizAquino

Qua Nov 02, 2011 11:15
Sequências
-
- Integral: converge ou diverge
por Victor Gabriel » Qui Abr 18, 2013 13:24
- 1 Respostas
- 1015 Exibições
- Última mensagem por Victor Gabriel

Dom Abr 21, 2013 12:03
Cálculo: Limites, Derivadas e Integrais
-
- [Série] Calcular valor de série tendo outra como referência
por robmenas » Dom Abr 07, 2019 14:35
- 0 Respostas
- 9189 Exibições
- Última mensagem por robmenas

Dom Abr 07, 2019 14:35
Sequências
-
- [série de Euler / problema da Basiléia] Série de Fourier
por Burnys » Qua Jul 16, 2008 14:34
- 4 Respostas
- 9084 Exibições
- Última mensagem por admin

Qui Jul 17, 2008 00:33
Sequências
-
- Integral: converge
por Victor Gabriel » Seg Abr 29, 2013 14:57
- 0 Respostas
- 880 Exibições
- Última mensagem por Victor Gabriel

Seg Abr 29, 2013 14:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.