Dois lados de um triângulo têm comprimentos a = 4cm e b = 3cm, mas estão crescendo a uma taxa de 1 cm/s. Se a área do triângulo permanece constante, a qual taxa está variando o ângulo alfa entre a e b quando alfa = pi/6.
Agradeço desde já quem puder ajudar!
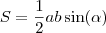
é a área, 
e 
os lados conhecidos e 
o ângulo entre eles.
, obtemos![\frac{\mathrm{d} S}{\mathrm{d} t} = \frac{1}{2}\frac{\mathrm{d} }{\mathrm{d} t}\left ( ab\sin \left ( \alpha \right ) \right ) = \frac{1}{2}\left [ \frac{\mathrm{d} (ab)}{\mathrm{d} t}\sin \left ( \alpha \right )+\cos \left ( \alpha \right ).\frac{\mathrm{d}\alpha }{\mathrm{d} t}ab \right ]](/latexrender/pictures/b2f0e27d38bc3f13123066341ed9de5a.png "\frac{\mathrm{d} S}{\mathrm{d} t} = \frac{1}{2}\frac{\mathrm{d} }{\mathrm{d} t}\left ( ab\sin \left ( \alpha \right ) \right ) = \frac{1}{2}\left [ \frac{\mathrm{d} (ab)}{\mathrm{d} t}\sin \left ( \alpha \right )+\cos \left ( \alpha \right ).\frac{\mathrm{d}\alpha }{\mathrm{d} t}ab \right ]")
.
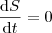. Isolando, então, a taxa de variação de 
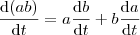obtemos, finalmente![\frac{\mathrm{d} \alpha }{\mathrm{d} t} = -\tan \left ( \alpha \right )\left [ \frac{1}{b}\frac{\mathrm{d} b}{\mathrm{d} t}+\frac{1}{a}\frac{\mathrm{d} a}{\mathrm{d} t} \right ]](/latexrender/pictures/6df2f19f4d950eab8c1bc78b67930516.png "\frac{\mathrm{d} \alpha }{\mathrm{d} t} = -\tan \left ( \alpha \right )\left [ \frac{1}{b}\frac{\mathrm{d} b}{\mathrm{d} t}+\frac{1}{a}\frac{\mathrm{d} a}{\mathrm{d} t} \right ]")
por