Pág. 98 Ex 63.
Seja
 , dada pela lei:
, dada pela lei: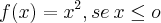
![f(x)={\sqrt[3]{x}, se\: x > 0 f(x)={\sqrt[3]{x}, se\: x > 0](/latexrender/pictures/a2455b4dc99eef6a1e241fb2db5b1487.png)
Determine:
![a)f\left(\left[-1,8 \right] \right) a)f\left(\left[-1,8 \right] \right)](/latexrender/pictures/afa68d887cebc422e84558482b3ebcfe.png)
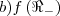
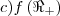
![d){f}^{-1}\left(\left[1,16 \right] \right) d){f}^{-1}\left(\left[1,16 \right] \right)](/latexrender/pictures/989317d84c47c73d21304d4074c40281.png)
![d){f}^{-1}\left(\left[-1,16 \right] \right) d){f}^{-1}\left(\left[-1,16 \right] \right)](/latexrender/pictures/efbf1bac123e281488ee54e8197a4200.png)

Se for possível, queria a resolução de apenas uma como exemplo, e uma explicação de como fazer as outras.
Minha dúvida é, por exemplo na a), fiz o gráfico das duas funções:
Não sei cmo fazer pra ele aparecer aqui.
Enfim, fiz o grafico, mas n sei cmo estudar ele.
SE puderem me ajudar agradeço.


