Tem duas integrais que eu não consegui resolver , a primeira:
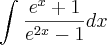
A primeira coisa que eu fiz foi simplifica a função ficando assim;
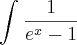
Dai eu tentei Integrar por partes substituindo
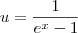
e dv=dx
A Segunda Integral q eu não consegui resolver foi essa daqui:
![\int_{}^{} \frac{1}{{x}^{3}}\sqrt[]{1 + \frac{1}{2x}} dx](/latexrender/pictures/68f2dbf77eea58693ba7b5fb7ba4d514.png "\int_{}^{} \frac{1}{{x}^{3}}\sqrt[]{1 + \frac{1}{2x}} dx")
Essa eu não sei nem como começar.Seria uma integral por partes tendo como dv =1/x³dx e u= ao restante?
no numerador dela (note que 0 é o elemento neutro da adição ) ,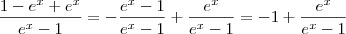 
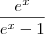é extamemte a derivada da expressão 
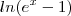não é verdade ?
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)