 por KleinIll » Sex Fev 22, 2013 11:30
por KleinIll » Sex Fev 22, 2013 11:30
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por young_jedi » Sex Fev 22, 2013 12:39
por young_jedi » Sex Fev 22, 2013 12:39
na verdade as duas maneiras que voce fez estão corretas
o que muda e o valor das constantes que aparacem na integração
em uma voce tem
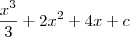
e na outra
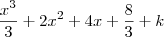
portanto
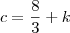
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por KleinIll » Sex Fev 22, 2013 12:57
por KleinIll » Sex Fev 22, 2013 12:57
Ok, então isto significa que dependendo do método pode haver uma constante diferente apesar da proposta de cada método ter a mesma meta?
Você pode explicar de uma forma simplificada o porquê da diferença da constante entre os métodos?
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por young_jedi » Sex Fev 22, 2013 19:09
por young_jedi » Sex Fev 22, 2013 19:09
na verdade quando voce calcula a integral voce vai ter tambem um valor constatnte em função da integraçao
o qual voce nao sabe qual é mais que pode ser determinado se o exercicio oferecer um dado adicional.
neste caso as duas resposta são soluções gerais da integral, ambas estão corretas.
a questão é a seguinte, na resposta do segundo metodo voce pode fazer o seguinte
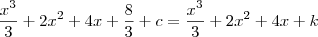
pois voce sabe que tanto

, com c, são constantes então voce pode espressa-las em uma mesma constatnte k
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por KleinIll » Sáb Fev 23, 2013 16:17
por KleinIll » Sáb Fev 23, 2013 16:17
young_jedi, eu entendo a sua explicação, mas o fato é que resolvendo o produto notável e depois integrando ou fazendo pelo método da substituição, teoricamente, deveriam alcançar os mesmos resultados, não concorda? Os resultados foram os mesmos, mas a diferença das constantes é, na minha opinião (eu não tenho certeza absoluta), uma distorção entre os métodos que eu desconheço a origem. Concordo com tudo que vc disse e entendo seu ponto de vista, mas, pelo sim ou pelo não, a diferença tem uma explicação além desta. Obrigado pela(s) ajuda(s), caiu como uma luva.
??? ?? ? ????, ? ? ??????.
-

KleinIll
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Qua Out 31, 2012 14:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Regra dos dois caminhos.
por Sobreira » Qua Fev 27, 2013 02:16
- 0 Respostas
- 2193 Exibições
- Última mensagem por Sobreira

Qua Fev 27, 2013 02:16
Cálculo: Limites, Derivadas e Integrais
-
- PROBLEMAS COM VARIAS RESPOSTAS
por dvr880 » Qua Nov 02, 2011 16:05
- 1 Respostas
- 1685 Exibições
- Última mensagem por mausim

Dom Nov 13, 2011 07:19
Matemática Financeira
-
- [funções log ln exponenciais] com respostas insolúveis
 por da Silva » Qua Nov 30, 2016 18:24
por da Silva » Qua Nov 30, 2016 18:24
- 2 Respostas
- 2626 Exibições
- Última mensagem por petras

Dom Dez 18, 2016 23:39
Equações
-
- [Duvida]Respostas diferentes e equivalentes, porque?
por Deivid » Ter Set 21, 2010 18:07
- 2 Respostas
- 1941 Exibições
- Última mensagem por Deivid

Qua Set 22, 2010 14:29
Cálculo: Limites, Derivadas e Integrais
-
- Dois Problemas De P.A
por Guedes » Sex Out 08, 2010 13:44
- 5 Respostas
- 4545 Exibições
- Última mensagem por Augusto Evaristo

Sex Out 15, 2010 23:40
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
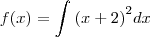
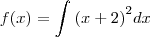
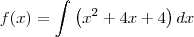
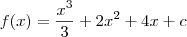
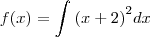
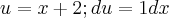
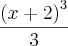
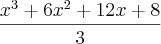
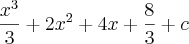

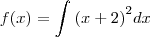
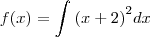
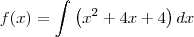
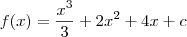
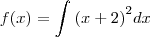
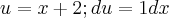
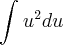
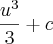
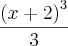
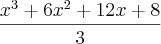
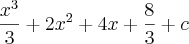

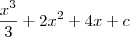
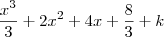
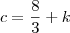


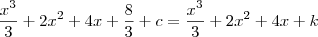
 , com c, são constantes então voce pode espressa-las em uma mesma constatnte k
, com c, são constantes então voce pode espressa-las em uma mesma constatnte k



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.