 por igorsch » Qua Jan 30, 2013 22:40
por igorsch » Qua Jan 30, 2013 22:40
[Porcentagem inversa]
Ola pessoal, tenho o seguinte problema.
Digamos que eu venda um produto no valor de R$ 100,00
Meu vendedor quer 10% de comissão
A princípio cobraria R$ 110,00 do cliente, mas não posso, pois no final o vendedor quer apenas pegar o valor total cobrado e descontar seus 10%.
Então preciso de uma formula a qual o resultado seja o número onde descontarei 10% e me sobre o valor de venda.
Em outras palavras: Tirar 10% do total e restar os meus R$ 100,00.
Grato pela atenção!
-
igorsch
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jan 30, 2013 22:28
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qui Jan 31, 2013 15:21
por young_jedi » Qui Jan 31, 2013 15:21
vamos dizer que esse valor é x
portanto
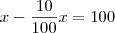
resolvendo a equação voce encontra o valor de x
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por igorsch » Qui Jan 31, 2013 18:12
por igorsch » Qui Jan 31, 2013 18:12
Certo amigo, desculpe minha falta de preparo ou talvez incapacidade, mas estudei isso já a muito tempo e não sei bem como resolver este tipo de equação, teria como apresentar um exemplo já resolvido? mostrando as operações de multiplicação, divisão e soma?
Muitíssimo obrigado.
-
igorsch
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jan 30, 2013 22:28
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qui Jan 31, 2013 20:18
por young_jedi » Qui Jan 31, 2013 20:18
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por igorsch » Sex Fev 01, 2013 03:26
por igorsch » Sex Fev 01, 2013 03:26
Perfeito, muitíssimo obrigado, entendi claramente, adimiro seu conhecimento. Grande Abraço!
-
igorsch
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jan 30, 2013 22:28
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por igorsch » Qua Fev 13, 2013 18:27
por igorsch » Qua Fev 13, 2013 18:27
Caros amigos.
Tentei aplicar esta formula de várias maneiras com valores diferente e parece não funcionar, se não for abusar da sua boa vontade, poderia mostra um exemplo com qualquer outro valor e porcentagem porexemplo, R$ 250,00 e 18%?
Grato pela atenção!
-
igorsch
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jan 30, 2013 22:28
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Qua Fev 13, 2013 18:41
por Cleyson007 » Qua Fev 13, 2013 18:41
Olá Igor, boa tarde!
Você montou assim
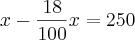
?
Resolvendo,
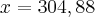
Comente qualquer dúvida

Até mais.
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Porcentagem] Fração mista e porcentagem
por Mayra Luna » Ter Fev 26, 2013 20:58
- 2 Respostas
- 4583 Exibições
- Última mensagem por Mayra Luna

Ter Fev 26, 2013 23:41
Álgebra Elementar
-
- Porcentagem - Porcentagem com minutos
por marcorrer » Qua Abr 04, 2012 13:52
- 6 Respostas
- 7912 Exibições
- Última mensagem por marcorrer

Seg Abr 09, 2012 16:25
Álgebra Elementar
-
- função inversa
por gisa123 » Qui Ago 28, 2008 17:22
- 1 Respostas
- 3407 Exibições
- Última mensagem por Molina

Qui Ago 28, 2008 23:53
Funções
-
- Tangente Inversa
por xducke » Qua Jul 22, 2009 02:34
- 1 Respostas
- 3256 Exibições
- Última mensagem por xducke

Qua Jul 22, 2009 18:19
Trigonometria
-
- Matriz Inversa
por Cleyson007 » Qui Ago 20, 2009 17:49
- 5 Respostas
- 4497 Exibições
- Última mensagem por Cleyson007

Sáb Ago 22, 2009 10:45
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



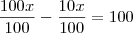
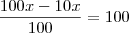
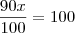
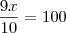
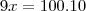

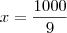
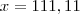
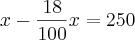 ?
?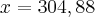


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.