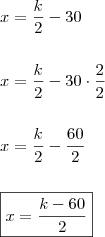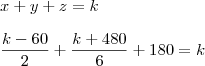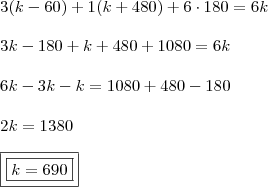Em determinado dia, todas as correspondências recebidas na agência dos Correios da cidade Alfa destinam-se apenas a moradores dos bairros X,Y e Z. Ao bairro X foi destinada metade das correspondências recebidas na agência menos 30 correspondências; ao bairro Y foi destinada terça parte das correspondências restantes, isto é, depois de retiradas as do bairro X, e mais 70 correspondências; o bairro Z recebeu 180 correspondências.
O total de correspondências recebidas, nesse dia, na agência dos correios da cidade Alfa foi
a/ Superior a 680 e inferior a 700
b) superior a 700 e inferior a 720
c) superior a 720
d) inferior a 660
e) superior a 660 e inferior a 680
Eu dividi os eventos em A, B e C, e o X vai ser o número de correspondências. Logo, A + B + C = x
A = x/2 - 30
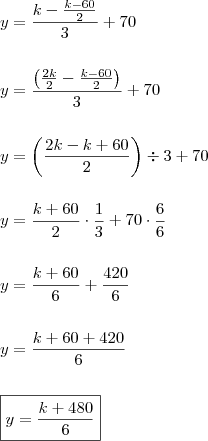
B = 1/3 (x - A) + 70
C = 180
A + B + C = X
x/2 - 30 + 1/3 (x - A) + 70 + 180 = x
x/2 - 30 + 1/3 (x -x/2 - 30) + 70 + 180 = x
Minha dúvida é nessa passagem, a prioridade são os parenteses, certo? E a soma ou subtração de frações tem que tirar o MMC, certo? MAS, eu faço o mmc só dos parenteses primeiros? Ou eu faço o MMC de todos os números fracionados? E depois de tirar o MMC eu divido e multiplico por todos os números?
Me ajudem por favor ! ! !
Certo dia, um Analista Judiciário digitou parte de um texto sobre legislação trabalhista. Ele executou essa tarefa em 24 minutos, de acordo com o seguinte procedimento:
- nos primeiros 8 minutos, digitou a quarta parte do texto e mais 1/4 de página;
- nos 8 minutos seguintes, a terça parte do número de páginas restantes e mais 1/3 de página;
- nos últimos 8 minutos, a metade do número de páginas restantes e mais 1/2 página.
Se, dessa forma, ele completou a tarefa, o total de páginas do texto era um número:
(A) Compreendido entre 15 e 20.
(B) Quadrado perfeito.
(C) Par
(D) Compreendido entre 1 e 10.
(E) Compreendido entre 10 e 15.
Novamente os procedimentos são A, B e C.
Se nos primeiros 8 minutos, ele digitou a quarta parte mais 1/4 de página, então:
A = x/4 + 1/4
Nos 8 minutos Seguintes, a terça parte do número de páginas restantes e mais 1/3 de página,ou seja, do que restou ele digitou isso, então:
B = ( x - A )/3 + 1/3
Terceira parte, a metade do número de páginas restantes e mais 1/2 página. Então:
C = [x - (A + B)]/2 + 1/2
A + B + C = X
x/4 + 1/4 + (X - A)/ 3 + 1/3 + X - (A + B)/2 + 1/2
Substituindo os valores de A e B
X/4 + 1/4 + (X - x/4 + 1/4)/3 + 1/3 + X - [( x/4 + 1/4 + x - x/4 + 1/4 + x - x/4 + 1/4)/3 + 1/3]/2 + 1/2
Olha sinceramente não sei nem se essa construção está certo e mesmo se tiver, eu tenho dúvidas por onde começar essas equações que tem frações e parenteses.
Alguém poderia me ajudar?
Abraço !