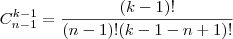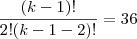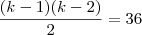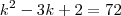por Vivian_G » Sáb Jan 26, 2013 15:22
por Vivian_G » Sáb Jan 26, 2013 15:22
Dada a equação x + x‚ + ... + xn = k, na qual k N, chama-se solução inteira dessa equação a toda n-pla de números inteiros (?,?‚, ..., ?n), tal que ? + ?‚ + ... + ?n = k. Assim, por exemplo, as ternas (6, 10, 3) e (-2, 9, 12) são soluções inteiras da equação x + y + z = 19. Sabe-se que o número de soluções inteiras e positivas da equação x + x‚ + ... + xn = k é dado pela combinação (C) de k - 1 elementos, n - 1 a n - 1. Nessas condições, se a equação x + y + z = k tem 36 soluções inteiras e positivas, então uma solução dessa equação é:
a) (2, 1, 3)
b) (4, 2, 3)
c) (3, 6, 1)
d) (5, 3, 4)
e) (8, 7, 5)
-
Vivian_G
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Jan 26, 2013 15:10
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Dom Jan 27, 2013 13:37
por young_jedi » Dom Jan 27, 2013 13:37
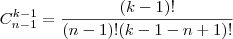
como nos temos tres termos então n=3 então
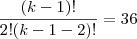
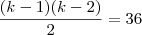
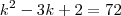

resolvendo por baskara ou soma e produto
k=-7 ou k=10
como k deve ser positivo então k igual a 10
a alternativa que satisfaz é a c)
pois
3+6+1=10
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [P.A.] Exercício
por Cleyson007 » Dom Mai 25, 2008 13:02
- 1 Respostas
- 6563 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 13:20
Progressões
-
- Exercício de PA
por Cleyson007 » Dom Jun 01, 2008 02:45
- 1 Respostas
- 11349 Exibições
- Última mensagem por admin

Dom Jun 01, 2008 14:31
Progressões
-
- Exercício de PA e PG
por Cleyson007 » Sáb Jun 14, 2008 01:21
- 3 Respostas
- 15309 Exibições
- Última mensagem por DanielFerreira

Sex Jul 24, 2009 11:59
Progressões
-
- exercicio de P.G.
por Gir » Qui Jul 02, 2009 18:21
- 3 Respostas
- 4428 Exibições
- Última mensagem por Gir

Sex Jul 03, 2009 10:12
Progressões
-
- exercicio de P.G.
por Gir » Seg Jul 06, 2009 10:54
- 1 Respostas
- 3376 Exibições
- Última mensagem por Marcampucio

Seg Jul 06, 2009 16:33
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.