renan_a escreveu:1 - descrever a equação do parabolóide de vértice na origem , sabendo que sua interseção com o plano z=4 é a circunferencia de C(0,0,4) e raio 3.
Como a interseção do paraboloide com o plano z = 4 é uma circunferência (e este paraboloide tem vértice na origem), temos que o formato de sua equação será:

Determinando a interseção desse paraboloide com o plano z = 4, obtemos:


Note que esta deve ser uma circunferência de raio 3 (sendo que seu centro já é (0, 0, 4)).
Agora tente concluir o exercício a partir daí.
renan_a escreveu:2- O traço de um elipsóide centrado na origem no plano xy é a elipse x^2 + y^2/4 = 1 , quando z=0 . Determinar a equação do elipsóide sabendo que contém o ponto (0,1,
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png)
)
Como o elipsoide está centrado na origem e sua interseção com o plano z = 0 é uma elipse, temos que sua equação está no formato:

Sabemos que sua interseção com o plano z = 0 é dada por:

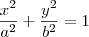
Por outro lado, foi dito que essa interseção é a elipse:

Disso concluímos que

e

. Falta então determinar

para completar a equação do elipsoide. Para isso, basta usar o fato de que o elipsoide contém o ponto

. Ou seja, podemos substituir esse ponto na equação do elipsoide.
Agora tente concluir o exercício a partir daí.
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png)
![\sqrt[]{6} \sqrt[]{6}](/latexrender/pictures/bd95d60cfbcfe62be13a43e39e60bbdb.png) )
)






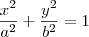

 e
e  . Falta então determinar
. Falta então determinar  para completar a equação do elipsoide. Para isso, basta usar o fato de que o elipsoide contém o ponto
para completar a equação do elipsoide. Para isso, basta usar o fato de que o elipsoide contém o ponto  . Ou seja, podemos substituir esse ponto na equação do elipsoide.
. Ou seja, podemos substituir esse ponto na equação do elipsoide.

 .
.



