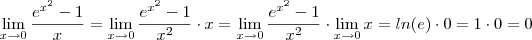por Jamyson » Dom Jan 13, 2013 16:34
por Jamyson » Dom Jan 13, 2013 16:34
Gente estou com muita dúvida neste limite, já tentei de varias maneiras resolver ele, mas ainda não consegui..
A resposta no livro do Guidorozzi é 0.
Já fiz uma mudança de Variável
![u = {e}^{{x}^{2}} - 1, \Rightarrow x = \sqrt[2]{Ln\left(u+1 \right)} u = {e}^{{x}^{2}} - 1, \Rightarrow x = \sqrt[2]{Ln\left(u+1 \right)}](/latexrender/pictures/afd4b8097237b3778caef9272066b225.png)
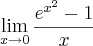
=
![\lim_{u\rightarrow0} = \frac{u}{\sqrt[2]{Ln\left(u+1 \right)}} \lim_{u\rightarrow0} = \frac{u}{\sqrt[2]{Ln\left(u+1 \right)}}](/latexrender/pictures/11c9965c82be6e19daa69f909751be08.png)
Eu cheguei um pouco mais longe, mas é complicado por aqui no site...
Se puderem me explicar, Agradeço..

-
Jamyson
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Jan 12, 2013 18:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Dom Jan 13, 2013 18:12
por e8group » Dom Jan 13, 2013 18:12
Boa tarde , multiplique o numerador e o denominador por

. Utilize a propriedade "
limite do produto é o produto dos limites " . Além disso , mostre que um destes produtos dos limites é 1(usando o limite fundamental
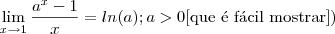
.E , o outro limite resulta zero .
Qualquer dúvida só postar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jamyson » Dom Jan 13, 2013 19:46
por Jamyson » Dom Jan 13, 2013 19:46
![\frac{u\sqrt[2]{Ln\left(u+1 \right)}}{Ln\left(u+1 \right)} \frac{u\sqrt[2]{Ln\left(u+1 \right)}}{Ln\left(u+1 \right)}](/latexrender/pictures/7db0008f5718d6f34dff69fb3180dc56.png)
Parei logo ai, já revisei umas propriedades logaritmos...
-
Jamyson
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Jan 12, 2013 18:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Dom Jan 13, 2013 20:15
por e8group » Dom Jan 13, 2013 20:15
Boa noite .Note que ,
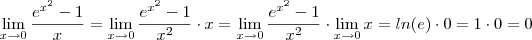
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jamyson » Dom Jan 13, 2013 23:04
por Jamyson » Dom Jan 13, 2013 23:04
Caramba, eu nunca iria resolver,
ObrigadO

-
Jamyson
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Jan 12, 2013 18:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4796 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4446 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
-
- Limite de funções
 por jeremiashenrique » Sex Abr 17, 2015 16:07
por jeremiashenrique » Sex Abr 17, 2015 16:07
- 1 Respostas
- 1629 Exibições
- Última mensagem por DanielFerreira

Sex Abr 17, 2015 20:32
Funções
-
- Limite de funções
 por jeremiashenrique » Sex Abr 17, 2015 16:07
por jeremiashenrique » Sex Abr 17, 2015 16:07
- 1 Respostas
- 1646 Exibições
- Última mensagem por adauto martins

Seg Abr 20, 2015 20:57
Funções
-
- Limite de funções
 por jeremiashenrique » Ter Abr 21, 2015 12:16
por jeremiashenrique » Ter Abr 21, 2015 12:16
- 2 Respostas
- 1723 Exibições
- Última mensagem por jeremiashenrique

Qui Abr 23, 2015 00:18
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![u = {e}^{{x}^{2}} - 1, \Rightarrow x = \sqrt[2]{Ln\left(u+1 \right)} u = {e}^{{x}^{2}} - 1, \Rightarrow x = \sqrt[2]{Ln\left(u+1 \right)}](/latexrender/pictures/afd4b8097237b3778caef9272066b225.png)
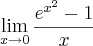 =
= ![\lim_{u\rightarrow0} = \frac{u}{\sqrt[2]{Ln\left(u+1 \right)}} \lim_{u\rightarrow0} = \frac{u}{\sqrt[2]{Ln\left(u+1 \right)}}](/latexrender/pictures/11c9965c82be6e19daa69f909751be08.png)


![u = {e}^{{x}^{2}} - 1, \Rightarrow x = \sqrt[2]{Ln\left(u+1 \right)} u = {e}^{{x}^{2}} - 1, \Rightarrow x = \sqrt[2]{Ln\left(u+1 \right)}](/latexrender/pictures/afd4b8097237b3778caef9272066b225.png)
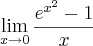 =
= ![\lim_{u\rightarrow0} = \frac{u}{\sqrt[2]{Ln\left(u+1 \right)}} \lim_{u\rightarrow0} = \frac{u}{\sqrt[2]{Ln\left(u+1 \right)}}](/latexrender/pictures/11c9965c82be6e19daa69f909751be08.png)


 . Utilize a propriedade "limite do produto é o produto dos limites " . Além disso , mostre que um destes produtos dos limites é 1(usando o limite fundamental
. Utilize a propriedade "limite do produto é o produto dos limites " . Além disso , mostre que um destes produtos dos limites é 1(usando o limite fundamental 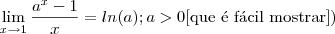 .E , o outro limite resulta zero .
.E , o outro limite resulta zero .
![\frac{u\sqrt[2]{Ln\left(u+1 \right)}}{Ln\left(u+1 \right)} \frac{u\sqrt[2]{Ln\left(u+1 \right)}}{Ln\left(u+1 \right)}](/latexrender/pictures/7db0008f5718d6f34dff69fb3180dc56.png)