![\int_\frac{sin(2x)}{\sqrt[]{1+sin²(x)}} dx](/latexrender/pictures/ad7395cf56accd4968f19cacaa48bb34.png "\int_\frac{sin(2x)}{\sqrt[]{1+sin²(x)}} dx")
Pessoal, essa integral não está sendo fácil pra mim.
Tentei chamar u=sin^2(x) , que me dá um du= 2sin(x)cos(x)dx = sin(2x) dx
então
![\int_ \frac{1}{\sqrt[]{1+u}} du](/latexrender/pictures/cc64f31568167ed6b60e29242cfd5ca7.png "\int_ \frac{1}{\sqrt[]{1+u}} du")
, se v=1+ u , dv= du , logo , ![\int_ \frac{1}{\sqrt[]{v}}](/latexrender/pictures/91102fa1a218f7634d975cbb13d09156.png "\int_ \frac{1}{\sqrt[]{v}}")
, que resolvendo me resulta em 2 ![\sqrt[]{1+u}](/latexrender/pictures/1d3b5e2855ba9a2048436e2e9d7b8329.png "\sqrt[]{1+u}")
= 2 ![\sqrt[]{1+ sin^2(x)}](/latexrender/pictures/67ac9325de017b3259583671fea3f8a7.png "\sqrt[]{1+ sin^2(x)}")
+ Cporém, o resultado está assim: 2
![\frac{\sqrt[]{(3-cos(2x)}^1/2}{2}](/latexrender/pictures/6153d9596c8af2dd3d8e24756d0521c3.png "\frac{\sqrt[]{(3-cos(2x)}^1/2}{2}")
(raiz elevada na um meio) .Essa resposta está sem simplicação acredito eu, porém o que eu não entendo, é aquela substituição do ( 1+sin^2(x) ) que está dentro da raíz...
Já no Wolfram alpha, a resposta correta é:
![\sqrt[]{(6-2cos(2x)}](/latexrender/pictures/fe592dce851a2a0e1abef12785aabbac.png "\sqrt[]{(6-2cos(2x)}")
+ C Agradeço desde já!
.Deste modo ,pela regra da cadeia .Vamos obter , ![\frac{d}{dx}\sqrt{sin^2(x) + 1} = \frac{d}{dx} \xi = \frac{d}{d(sin^2(x)+1)}[{sin^2(x) + 1}]^{1/2}\cdot \frac{d}{dx}(sin^2(x)+1) = \frac{1}{2\sqrt{sin^2(x)+1}} \cdot \frac{d}{d(sin(x))}sin^2(x) \frac{d}{dx}sin(x) = \frac{sin(x)cos(x)}{\sqrt{sin^2(x)+1}}](/latexrender/pictures/74c9bd9905def9efce600899e72511cf.png "\frac{d}{dx}\sqrt{sin^2(x) + 1} = \frac{d}{dx} \xi = \frac{d}{d(sin^2(x)+1)}[{sin^2(x) + 1}]^{1/2}\cdot \frac{d}{dx}(sin^2(x)+1) = \frac{1}{2\sqrt{sin^2(x)+1}} \cdot \frac{d}{d(sin(x))}sin^2(x) \frac{d}{dx}sin(x) = \frac{sin(x)cos(x)}{\sqrt{sin^2(x)+1}}")
. 
. 
. 
. 
.
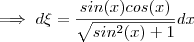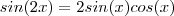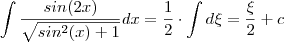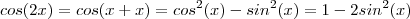
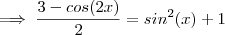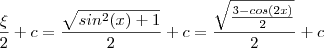, avisa que eu resolvo.
