 por guisaulo » Seg Dez 10, 2012 14:56
por guisaulo » Seg Dez 10, 2012 14:56
Estive tentando fazer esse exercício, porém não consegui resolver até um certo ponto.
Abaixo tá o comando da atividade e a minha resolução.
Queria que alguém me ajudasse a resolve-lo e corrigir alguma falha de calculo.
Calcule
![\int_{1}^{e}\sqrt[]{1+{(\frac{dx}{dy}})^{2}}dy \int_{1}^{e}\sqrt[]{1+{(\frac{dx}{dy}})^{2}}dy](/latexrender/pictures/0f86e02d270fbfd1c3b8919d593a1fa2.png)
, em que
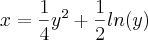
.
Primeiro eu calculei a derivada de x:
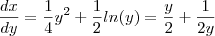
Depois eu substitui na equação da integral:
![\int_{1}^{e}\sqrt[]{1+{(\frac{y}{2}+\frac{1}{2y}})^{2}}dy \int_{1}^{e}\sqrt[]{1+{(\frac{y}{2}+\frac{1}{2y}})^{2}}dy](/latexrender/pictures/09d9e8652cbb37fa7566f8bb7a293b56.png)
![\int_{1}^{e}\sqrt[]{1+{(\frac{y^2}{4}+\frac{1}{4y^2}})}dy \int_{1}^{e}\sqrt[]{1+{(\frac{y^2}{4}+\frac{1}{4y^2}})}dy](/latexrender/pictures/28f5a8e943a68d2d4374cd5eb09cff7c.png)
Não achei uma maneira para calcular a integral a partir daqui.
-
guisaulo
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Nov 27, 2012 21:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral definida
por exploit » Ter Set 07, 2010 19:17
- 4 Respostas
- 3637 Exibições
- Última mensagem por exploit

Qua Set 08, 2010 19:58
Cálculo: Limites, Derivadas e Integrais
-
- integral definida
por liviabgomes » Qua Jun 01, 2011 15:14
- 8 Respostas
- 5959 Exibições
- Última mensagem por carlosalesouza

Qui Jun 02, 2011 12:38
Cálculo: Limites, Derivadas e Integrais
-
- integral definida
por liviabgomes » Qua Jun 01, 2011 15:14
- 2 Respostas
- 1501 Exibições
- Última mensagem por LuizAquino

Qui Jun 02, 2011 14:21
Cálculo: Limites, Derivadas e Integrais
-
- Integral Definida
por ah001334 » Seg Out 17, 2011 13:08
- 8 Respostas
- 3125 Exibições
- Última mensagem por LuizAquino

Ter Out 18, 2011 16:15
Cálculo: Limites, Derivadas e Integrais
-
- integral definida
por ferdinandaa » Seg Nov 28, 2011 14:29
- 1 Respostas
- 1505 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 17:22
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{1}^{e}\sqrt[]{1+{(\frac{dx}{dy}})^{2}}dy \int_{1}^{e}\sqrt[]{1+{(\frac{dx}{dy}})^{2}}dy](/latexrender/pictures/0f86e02d270fbfd1c3b8919d593a1fa2.png) , em que
, em que 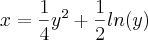 .
.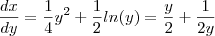
![\int_{1}^{e}\sqrt[]{1+{(\frac{y}{2}+\frac{1}{2y}})^{2}}dy \int_{1}^{e}\sqrt[]{1+{(\frac{y}{2}+\frac{1}{2y}})^{2}}dy](/latexrender/pictures/09d9e8652cbb37fa7566f8bb7a293b56.png)
![\int_{1}^{e}\sqrt[]{1+{(\frac{y^2}{4}+\frac{1}{4y^2}})}dy \int_{1}^{e}\sqrt[]{1+{(\frac{y^2}{4}+\frac{1}{4y^2}})}dy](/latexrender/pictures/28f5a8e943a68d2d4374cd5eb09cff7c.png)


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.