 por moraes1321 » Sáb Dez 01, 2012 10:49
por moraes1321 » Sáb Dez 01, 2012 10:49
sera que poderia me ajudar nesta questão!!!
Duas torres têm, respectivamente, 50 e 30 metros de altura, estando separadas por uma
distância de 150 metros e um cabo guia deve ser estendido do ponto A até o topo de cada torre.
(a) Localize exatamente o ponto A de modo que o comprimento total do cabo seja mínimo.
resposta e X=93,75
-
moraes1321
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Dez 01, 2012 10:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari civil
- Andamento: cursando
 por e8group » Sáb Dez 01, 2012 12:06
por e8group » Sáb Dez 01, 2012 12:06
Veja afigura em anexo ,
.
Pela visão geométrica vamos ter ,


.
Mas ,
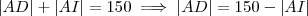
.Sejam ,
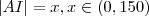
e

. Desta forma ,
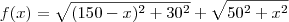
.
Agora tente concluir .
Como resultado eu deixo o seguinte link
http://www.wolframalpha.com/input/?i=mi ... 2+%7D++%7D.Faça uma comparação com o gabarito .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por moraes1321 » Ter Dez 04, 2012 22:10
por moraes1321 » Ter Dez 04, 2012 22:10
mas como faco agora para poder resolver esta funcao.
nao to conseguindo me ajuada ai
-
moraes1321
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Dez 01, 2012 10:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo Maximos e Minimos
por brunnoguilherme » Dom Jan 13, 2013 19:58
- 0 Respostas
- 1494 Exibições
- Última mensagem por brunnoguilherme

Dom Jan 13, 2013 19:58
Cálculo: Limites, Derivadas e Integrais
-
- Calculo III - Máximos e Minimos
por lukeibol » Seg Mai 08, 2017 14:47
- 0 Respostas
- 1253 Exibições
- Última mensagem por lukeibol

Seg Mai 08, 2017 14:47
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo I] Exercício - Máximos e Mínimos
por Pessoa Estranha » Dom Nov 16, 2014 11:43
- 3 Respostas
- 2542 Exibições
- Última mensagem por felipederaldino

Qui Nov 27, 2014 11:28
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo I] Exercício - Máximos e Mínimos
por Pessoa Estranha » Dom Nov 16, 2014 16:53
- 0 Respostas
- 1873 Exibições
- Última mensagem por Pessoa Estranha

Dom Nov 16, 2014 16:53
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo 1] Máximos e mínimos de uma função
por LuisLemos » Qua Jul 27, 2016 21:27
- 4 Respostas
- 6883 Exibições
- Última mensagem por LuisLemos

Qui Jul 28, 2016 00:49
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




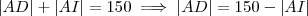 .Sejam ,
.Sejam , 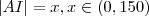 e
e  . Desta forma ,
. Desta forma , 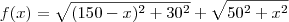 .
. 


 , avisa que eu resolvo.
, avisa que eu resolvo.

