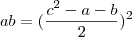por moraes1321 » Ter Dez 04, 2012 17:43
por moraes1321 » Ter Dez 04, 2012 17:43
Como faço para cacular esta função? ?((150-x)^2+30^2) + ?(50^2+x^2) =170?
a resposta de x=375/4
-
moraes1321
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Dez 01, 2012 10:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenhari civil
- Andamento: cursando
 por Russman » Ter Dez 04, 2012 19:13
por Russman » Ter Dez 04, 2012 19:13
Você vai ter de ir elevando ao quadrado até se livrar da raiz quadrada.
Temos algo do tipo:
![\sqrt[]{a} + \sqrt[]{b} = c \sqrt[]{a} + \sqrt[]{b} = c](/latexrender/pictures/e0537a7ec2d97e2bc17d03d2994dc73c.png)
Elevando ao quadrado em ambos lados:
![(\sqrt[]{a} + \sqrt[]{b})^2 = c^2 (\sqrt[]{a} + \sqrt[]{b})^2 = c^2](/latexrender/pictures/96b9c3a4166d05844c99812d66aaf1ff.png)
![\sqrt[]{a}\sqrt[]{a} + 2\sqrt[]{a}\sqrt[]{b} + \sqrt[]{b}\sqrt[]{b} = c^2 \sqrt[]{a}\sqrt[]{a} + 2\sqrt[]{a}\sqrt[]{b} + \sqrt[]{b}\sqrt[]{b} = c^2](/latexrender/pictures/1b8b571a82bc68a84964d53a427dd8dd.png)
![a + 2\sqrt[]{ab} + b = c^2 a + 2\sqrt[]{ab} + b = c^2](/latexrender/pictures/7de2640a04e495cd9df58a2846326f34.png)
Agora isole a raiz que sobrou:
![2\sqrt[]{ab} = c^2 - a - b 2\sqrt[]{ab} = c^2 - a - b](/latexrender/pictures/030fe7d34cf01798ebcbbc31a5dada4f.png)
![(\sqrt[]{ab})^2 = (\frac{c^2-a-b}{2})^2 (\sqrt[]{ab})^2 = (\frac{c^2-a-b}{2})^2](/latexrender/pictures/fb5c284d0b421e991d44b9ee4886c72d.png)
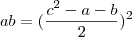
Pronto, você se livrou da raíz quadrada.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função] isso é função do segundo grau?
por maulakalanata » Qua Mar 27, 2013 04:03
- 1 Respostas
- 2287 Exibições
- Última mensagem por timoteo

Qua Mar 27, 2013 10:51
Funções
-
- [Função 1°grau] determinar função.
por Thiago 86 » Ter Abr 23, 2013 11:27
- 2 Respostas
- 2412 Exibições
- Última mensagem por Thiago 86

Ter Abr 23, 2013 13:05
Funções
-
- Função do 2° Grau
por mimi2009 » Qua Jun 10, 2009 05:46
- 1 Respostas
- 2091 Exibições
- Última mensagem por Molina

Qua Jun 10, 2009 08:05
Funções
-
- Função do 2 grau...
por Fiel8 » Qua Jul 01, 2009 21:34
- 4 Respostas
- 3448 Exibições
- Última mensagem por Cleyson007

Qui Jul 02, 2009 16:16
Funções
-
- Função 1° grau
por DanielFerreira » Ter Set 22, 2009 14:14
- 2 Respostas
- 2142 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 19:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![\sqrt[]{a} + \sqrt[]{b} = c \sqrt[]{a} + \sqrt[]{b} = c](/latexrender/pictures/e0537a7ec2d97e2bc17d03d2994dc73c.png)
![(\sqrt[]{a} + \sqrt[]{b})^2 = c^2 (\sqrt[]{a} + \sqrt[]{b})^2 = c^2](/latexrender/pictures/96b9c3a4166d05844c99812d66aaf1ff.png)
![\sqrt[]{a}\sqrt[]{a} + 2\sqrt[]{a}\sqrt[]{b} + \sqrt[]{b}\sqrt[]{b} = c^2 \sqrt[]{a}\sqrt[]{a} + 2\sqrt[]{a}\sqrt[]{b} + \sqrt[]{b}\sqrt[]{b} = c^2](/latexrender/pictures/1b8b571a82bc68a84964d53a427dd8dd.png)
![a + 2\sqrt[]{ab} + b = c^2 a + 2\sqrt[]{ab} + b = c^2](/latexrender/pictures/7de2640a04e495cd9df58a2846326f34.png)
![2\sqrt[]{ab} = c^2 - a - b 2\sqrt[]{ab} = c^2 - a - b](/latexrender/pictures/030fe7d34cf01798ebcbbc31a5dada4f.png)
![(\sqrt[]{ab})^2 = (\frac{c^2-a-b}{2})^2 (\sqrt[]{ab})^2 = (\frac{c^2-a-b}{2})^2](/latexrender/pictures/fb5c284d0b421e991d44b9ee4886c72d.png)