 por Lucio » Sex Nov 30, 2012 07:26
por Lucio » Sex Nov 30, 2012 07:26
Seja a equação exponencial

. Qual é a solução desta equação?
Resp: 3 < x < 8
Tentei resolver assim:





Mas não consigo chegar a resposta.
Onde estou errando? Está tudo errado?
Desde já agradeço a ajuda de todos
Abraços
-
Lucio
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Dez 21, 2011 07:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por e8group » Sex Nov 30, 2012 08:54
por e8group » Sex Nov 30, 2012 08:54
Bom dia .você cometeu erro no seguinte passo

. Note que

, deste modo

.Além disso ,observe que

.
Conforme sua expressão ,

.Tome cuidado em assumir que
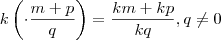
.Isto não é verdade .
EX.: Numerico :

Absurdo(8=14)!!! .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lucio » Sex Nov 30, 2012 16:11
por Lucio » Sex Nov 30, 2012 16:11
Santhiago muito obrigado pela sua assistência e pela dica.
Mas mesmo assim não estou conseguindo calcular a equação.
Você pode por favor, me auxiliar mais uma vez nessa resolução?
Abraços
-
Lucio
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Dez 21, 2011 07:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por e8group » Sex Nov 30, 2012 21:03
por e8group » Sex Nov 30, 2012 21:03
Claro ,com certeza .

Agora , se multiplicarmos ambos lados por
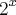
não alteraremos a igualdade . E , utilizando as propriedades

e

.Vamos obter ,

Agora observe as propriedades citadas acima e tente aplicar na equação acima , feito isto vamos obter :

Somando o simétrico de

em ambos lados , vamos ter
![(2^x)^2 -2^8 = 2^x\cdot 24 \leftrightarrow [ (2^x)^2 -2^8]+(-2^x\cdot 24) = 2^x\cdot 24 - 2^x\cdot 24 \leftrightarrow (2^x)^2 -2^x\cdot 24 -2^8 = 0 (2^x)^2 -2^8 = 2^x\cdot 24 \leftrightarrow [ (2^x)^2 -2^8]+(-2^x\cdot 24) = 2^x\cdot 24 - 2^x\cdot 24 \leftrightarrow (2^x)^2 -2^x\cdot 24 -2^8 = 0](/latexrender/pictures/3b2d55db9be25ac3bb6ff0162dd61d99.png)
Agora seja ,

. Como
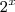
é estritamente positivo para quaisquer valores reais que

assumir (verifique ! ) vamos ter que ,

se e somente se
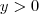
. Uma vez que temos solução para

teremos para

.
Resolvendo

.
Deste modo ,

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lucio » Sáb Dez 01, 2012 05:51
por Lucio » Sáb Dez 01, 2012 05:51
Olá Santhiago
Não sei como agradecer a sua ajuda, estudar sozinho é muito difícil. Vcs da AJUDAMATEMATICA são um grande apoio para isso.
Valeu msm
Um abraços
-
Lucio
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Dez 21, 2011 07:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equaçoes exponenciais
por natanskt » Qui Out 07, 2010 13:37
- 7 Respostas
- 4576 Exibições
- Última mensagem por Rogerio Murcila

Qui Out 07, 2010 17:25
Funções
-
- equaçoes exponenciais
por natanskt » Qui Out 07, 2010 13:58
- 6 Respostas
- 3785 Exibições
- Última mensagem por MarceloFantini

Qui Out 07, 2010 17:43
Funções
-
- equações com exponenciais
por Regina » Sex Fev 25, 2011 14:52
- 4 Respostas
- 3207 Exibições
- Última mensagem por Regina

Sex Fev 25, 2011 19:39
Logaritmos
-
- Equações Exponenciais
por umaiafilho » Qui Mai 12, 2011 21:09
- 2 Respostas
- 2352 Exibições
- Última mensagem por umaiafilho

Qui Mai 12, 2011 23:01
Sistemas de Equações
-
- Equações Exponenciais
 por AlexKidd » Dom Ago 12, 2012 12:40
por AlexKidd » Dom Ago 12, 2012 12:40
- 5 Respostas
- 3852 Exibições
- Última mensagem por DanielFerreira

Seg Ago 27, 2012 20:42
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Qual é a solução desta equação?
. Qual é a solução desta equação?





 . Qual é a solução desta equação?
. Qual é a solução desta equação?





 . Note que
. Note que  , deste modo
, deste modo  .Além disso ,observe que
.Além disso ,observe que  .
.  .Tome cuidado em assumir que
.Tome cuidado em assumir que 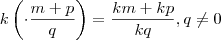 .Isto não é verdade .
.Isto não é verdade . 



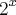 não alteraremos a igualdade . E , utilizando as propriedades
não alteraremos a igualdade . E , utilizando as propriedades  e
e  .Vamos obter ,
.Vamos obter , 

 em ambos lados , vamos ter
em ambos lados , vamos ter ![(2^x)^2 -2^8 = 2^x\cdot 24 \leftrightarrow [ (2^x)^2 -2^8]+(-2^x\cdot 24) = 2^x\cdot 24 - 2^x\cdot 24 \leftrightarrow (2^x)^2 -2^x\cdot 24 -2^8 = 0 (2^x)^2 -2^8 = 2^x\cdot 24 \leftrightarrow [ (2^x)^2 -2^8]+(-2^x\cdot 24) = 2^x\cdot 24 - 2^x\cdot 24 \leftrightarrow (2^x)^2 -2^x\cdot 24 -2^8 = 0](/latexrender/pictures/3b2d55db9be25ac3bb6ff0162dd61d99.png)
 . Como
. Como 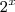 é estritamente positivo para quaisquer valores reais que
é estritamente positivo para quaisquer valores reais que  assumir (verifique ! ) vamos ter que ,
assumir (verifique ! ) vamos ter que ,  se e somente se
se e somente se 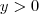 . Uma vez que temos solução para
. Uma vez que temos solução para  teremos para
teremos para  .
.  .
.  .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
