 por karen » Ter Nov 27, 2012 20:41
por karen » Ter Nov 27, 2012 20:41
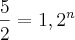
Dados: log2 = 0,30 e log 3 = 0,48
Tentei aplicar log dos dois lados, mas não vi nada que me ajudasse a descobrir n.
-
karen
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Mai 03, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrônica
- Andamento: formado
 por e8group » Ter Nov 27, 2012 22:03
por e8group » Ter Nov 27, 2012 22:03
Note que ,
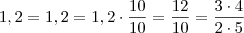
.
Logo ,
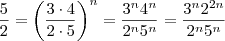
.
Multiplicando ambos lados por
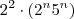
,vamos obter
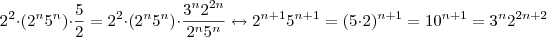
.
Aplicando logaritmo , vem que
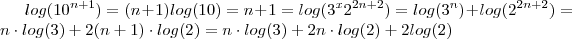
.
Somando

ambos lados e colocando o fator

em evidência ,
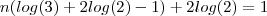
Somando
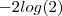
nos dois lados e após isto multiplicando por
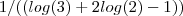
,vamos obter que ,
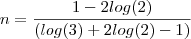
Basta susbstituir os valores aproximados de
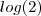
e
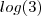
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por karen » Qua Nov 28, 2012 14:41
por karen » Qua Nov 28, 2012 14:41
Trabalhoso!
Muito obrigada =)
-
karen
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Mai 03, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrônica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2577 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1856 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2746 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo (UF-CE)
por JailsonJr » Sáb Mai 22, 2010 04:56
- 6 Respostas
- 5283 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:32
Logaritmos
-
- Logaritmo
por nan_henrique » Sex Jul 09, 2010 18:38
- 1 Respostas
- 2286 Exibições
- Última mensagem por Elcioschin

Sex Jul 09, 2010 19:42
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
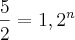

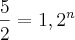

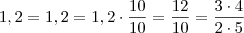 .
. 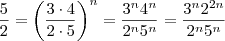 .
.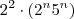 ,vamos obter
,vamos obter 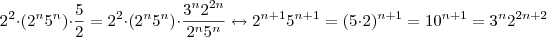 .
. 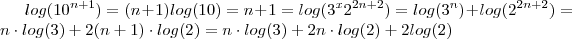 .
.  ambos lados e colocando o fator
ambos lados e colocando o fator  em evidência ,
em evidência , 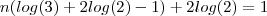
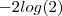 nos dois lados e após isto multiplicando por
nos dois lados e após isto multiplicando por 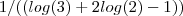 ,vamos obter que ,
,vamos obter que , 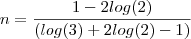
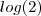 e
e 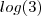 .
.

