Matriz
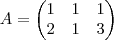
Matriz

Matriz
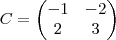
Pretende-se determinar a matriz X:
![\frac{1}{3}(AB^T + X)=2CI+\frac{1}{6}[(A+X)-A] \frac{1}{3}(AB^T + X)=2CI+\frac{1}{6}[(A+X)-A]](/latexrender/pictures/ad55d48f31dfd97596819d25796241b9.png)

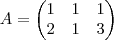

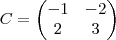
![\frac{1}{3}(AB^T + X)=2CI+\frac{1}{6}[(A+X)-A] \frac{1}{3}(AB^T + X)=2CI+\frac{1}{6}[(A+X)-A]](/latexrender/pictures/ad55d48f31dfd97596819d25796241b9.png)



 , disso temos
, disso temos 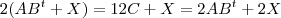 .
. 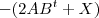 nos dois lados , vamos obter
nos dois lados , vamos obter  .
. 

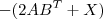 dos dois lados, como chegamos a essa conclusão?
dos dois lados, como chegamos a essa conclusão?
.Sherminator escreveu:Bom dia, muito obrigado pela explicação, eu tinha tentado fazer, mas nunca conseguia chegar a um resultado, não estava mesmo conseguindo, assim vendo como se faz, futuramente já será mais fácil
Só não entendi o porquê de somardos dois lados, como chegamos a essa conclusão?
 . Para isto ,temos que ter apenas ela em um dos lados da igualdade em função das outras matrizes e para conseguirmos isso temos que adicionar uma mesma matriz em ambos da igualdade lados tal que obtemos
. Para isto ,temos que ter apenas ela em um dos lados da igualdade em função das outras matrizes e para conseguirmos isso temos que adicionar uma mesma matriz em ambos da igualdade lados tal que obtemos  .
. 
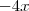 nos dois lados ,
nos dois lados , 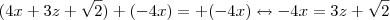 .
. 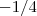 , vamos obter
, vamos obter 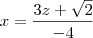 .
.  em função de
em função de  , para cada valor que
, para cada valor que  assumir temos o seu correspondente
assumir temos o seu correspondente  que satisfaz
que satisfaz  .
. 


Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)