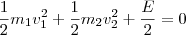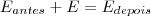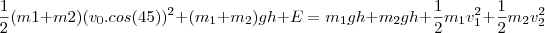FAP0151
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Russman » Ter Nov 20, 2012 22:47
por Russman » Ter Nov 20, 2012 22:47
Pessoal, não consigo ver o que falta considerar pra terminar a seguinte questão:
Um projétil é disparado a um ângulo de 45° com energia cinética inicial E. No topo da trajetória, o projétil o projétil explode com energia adicional E em dois fragmentos. Um fragmento de massa m1 viaja diretamente para baixo. Qual é a velocidade (módulo e direção) do segundo fragmento de massa m2 e velocidade do primeiro fragmento? Qual é a maior razão possível m1/m2?
====================
Visto que a componente horizontal do momento linear se conserva, temos:
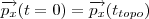
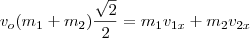
como
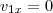
, então
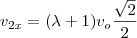
onde
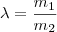
.
Agora eu não consigo entender o que significa a energia adicional pra aplicar a conservação de energia. ;x
Alguém ajuda?
Obrigado.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MarceloFantini » Qua Nov 21, 2012 01:25
por MarceloFantini » Qua Nov 21, 2012 01:25
Vamos ver o que conseguimos, parece um pouco complicada.
Pela conservação de energia temos que
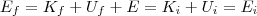
, onde
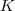
representa a cinética e
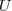
representa a potencial. No lançamento, adotando o plano de lançamento como referência, temos que
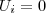
e
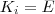
.
Na explosão as duas massas tem a mesma energia potencial pois estão à mesma altura, logo
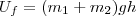
. Como a altura máxima é dada por
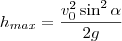
segue que
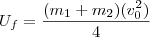
, pois
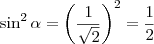
, que multiplicou o 2 no denominador.
A energia cinética final torna-se
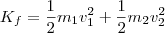
, logo concluímos que
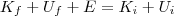
vira
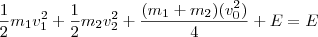
.
Como a energia cinética inicial é igual a
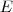
podemos escrever
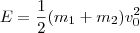
, assim
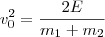
. Substituindo na expressão acima, chegamos que
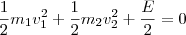
ou
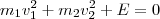
.
Pelo enunciado a velocidade horizontal do projétil 1 é nula, logo
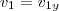
.
Estou um pouco cansado e tentei avançar mais que isso aqui, só que está difícil. Primeiramente pareceu que o ângulo de

era o mesmo do lançamento, porém com norma maior por causa da energia adicional. Neste caso é como se
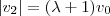
como definiu, mas se você abrir as contas com a expressão que deduzi encontrará
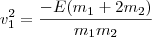
.
Por enquanto é só o que consegui, vou tentar fazer mais alguma coisa amanhã. Espero que já ajude.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Russman » Qua Nov 21, 2012 08:11
por Russman » Qua Nov 21, 2012 08:11
Pois é, Marcelo. Pensei da mesma forma que você. Mas a expressão
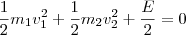
não pode ser verdade, pois todas as parcelas são positivas. ;x
O
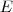
é a energia cinética inicial do projétil, que é positiva sempre.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qua Nov 21, 2012 08:17
por Russman » Qua Nov 21, 2012 08:17
Eu pensei em fazer uma relação entre a energia mecânica antes e depois da explosão.
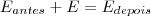
Eu penso em colocar o
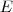
junto com a energia anterior pq é devido a ela que se tem a explosão.
Então:
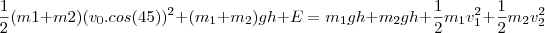
e agora eu tenho que desenvolver...
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MarceloFantini » Qua Nov 21, 2012 11:02
por MarceloFantini » Qua Nov 21, 2012 11:02
Você tem razão, a expressão é inválida. Mas estou discordando da sua expressão também. A energia cinética inicial leva em conta o módulo total, não apenas o módulo na horizontal. Além disso, tomando o chão como referência a energia potencial anula-se.
A menos que o instante que você considerando é exatamente antes da explosão, caso em que as energias potenciais final e inicial serão iguais, correto? Afinal de contas, antes que as partículas espalhem-se elas estão à mesma altura.
Isto é uma questão de física 1?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Russman » Qua Nov 21, 2012 14:35
por Russman » Qua Nov 21, 2012 14:35
É verdade. Eu estou considerando energias que não existem no topo.
Eu estou considerando as energias antes e depois da explosão.
É uma questão de Mecânica Clássica.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Neperiano » Qua Nov 21, 2012 16:50
por Neperiano » Qua Nov 21, 2012 16:50
Olá
Senhores, neste caso vocês podem considerar explosão como uma colisao, por tanto trata-se de uma questão de colisão e conservação de energia.
Você provavelmente terá que usar a conservação do momento linear: pi = pf, e a conservação da energia mecância: Emi = Emf, como não há evidências de atrito.
Entretanto está inclinado, portanto terá que usar um pouco de álgebra tambem, minha sugestão é tu montar o problema desenhando ele, e ai tu vai tem que inclinar ele para x e para y se for necessário.
Att
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Fundamentos de Mecânica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Física
por Mi_chelle » Qua Abr 13, 2011 17:52
- 3 Respostas
- 5030 Exibições
- Última mensagem por Mi_chelle

Qui Abr 14, 2011 00:07
Números Complexos
-
- física
 por leticiapires52 » Sáb Mar 28, 2015 20:10
por leticiapires52 » Sáb Mar 28, 2015 20:10
- 0 Respostas
- 1195 Exibições
- Última mensagem por leticiapires52

Sáb Mar 28, 2015 20:10
Estatística
-
- Questão de Física
por Kelvin Brayan » Dom Mar 06, 2011 19:51
- 2 Respostas
- 9319 Exibições
- Última mensagem por Igor Mirandola

Sex Out 28, 2011 22:57
Cálculo: Limites, Derivadas e Integrais
-
- Questão de Física
por valeuleo » Sáb Mai 28, 2011 16:03
- 2 Respostas
- 3030 Exibições
- Última mensagem por valeuleo

Sáb Mai 28, 2011 16:29
Funções
-
- Calculo de fisica
 por andersontricordiano » Sex Jul 01, 2011 17:13
por andersontricordiano » Sex Jul 01, 2011 17:13
- 1 Respostas
- 1903 Exibições
- Última mensagem por Neperiano

Sex Jul 01, 2011 18:40
Física
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
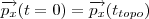
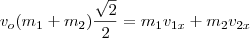
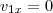 , então
, então 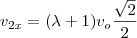 onde
onde 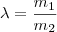 .
.

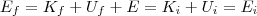 , onde
, onde 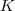 representa a cinética e
representa a cinética e 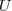 representa a potencial. No lançamento, adotando o plano de lançamento como referência, temos que
representa a potencial. No lançamento, adotando o plano de lançamento como referência, temos que 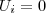 e
e 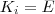 .
. 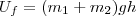 . Como a altura máxima é dada por
. Como a altura máxima é dada por 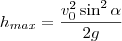 segue que
segue que  , pois
, pois 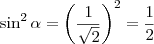 , que multiplicou o 2 no denominador.
, que multiplicou o 2 no denominador.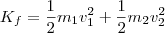 , logo concluímos que
, logo concluímos que 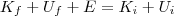 vira
vira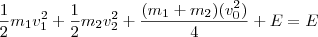 .
.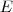 podemos escrever
podemos escrever 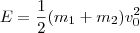 , assim
, assim 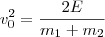 . Substituindo na expressão acima, chegamos que
. Substituindo na expressão acima, chegamos que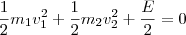 ou
ou 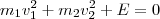 .
.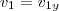 .
. era o mesmo do lançamento, porém com norma maior por causa da energia adicional. Neste caso é como se
era o mesmo do lançamento, porém com norma maior por causa da energia adicional. Neste caso é como se 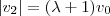 como definiu, mas se você abrir as contas com a expressão que deduzi encontrará
como definiu, mas se você abrir as contas com a expressão que deduzi encontrará 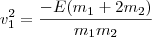 .
.