 por GABRIELA » Seg Set 21, 2009 17:25
por GABRIELA » Seg Set 21, 2009 17:25
A seguinte questão:
3x + y = -4
2x + 5y= 6
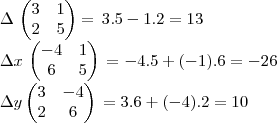
Não sei se esses cálculos estão corretos.O

encontrei, mas o
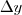
não esta correto. Onde está meu erro?
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Set 21, 2009 19:53
por Molina » Seg Set 21, 2009 19:53
Olá Gabriela.
O

está com as colunas trocadas. Refaça invertendo-as. A resposta que você irá obter é 26.
Quanto ao
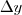
está montado corretamente, só que na hora de você fazer as operações está se condundindo:

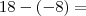
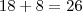
Entendeu?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por GABRIELA » Seg Set 21, 2009 21:00
por GABRIELA » Seg Set 21, 2009 21:00
molina escreveu:Olá Gabriela.
O

está com as colunas trocadas. Refaça invertendo-as. A resposta que você irá obter é 26.
Quanto ao
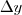
está montado corretamente, só que na hora de você fazer as operações está se condundindo:

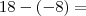
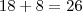
Entendeu?

Entendi sim!
Agora as respostas na apostila diz ser -2 e 2 por isso coloquei daquele jeito para que o resultado fique negativo
(-26)..Então minha apostila está errada?
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Set 21, 2009 23:43
por Molina » Seg Set 21, 2009 23:43
Pelo o que eu tinha feito,

mesmo:
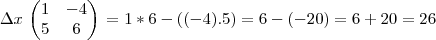
Certo?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por GABRIELA » Ter Set 22, 2009 09:45
por GABRIELA » Ter Set 22, 2009 09:45
molina escreveu:Pelo o que eu tinha feito,

mesmo:
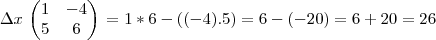
Certo?

Ok!
Inclusive,quando vai montar o

, na apostila ensina a fazer o inverso como tinha feito naprimeira vez.Ai acho as respostas igual lá.
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas
por Jansen » Dom Mai 10, 2009 00:01
- 5 Respostas
- 4707 Exibições
- Última mensagem por Molina

Seg Mai 11, 2009 04:36
Sistemas de Equações
-
- sistemas
por Magda » Sex Jun 19, 2009 18:37
- 5 Respostas
- 3746 Exibições
- Última mensagem por Magda

Sex Ago 07, 2009 19:49
Sistemas de Equações
-
- Sistemas...
por GABRIELA » Ter Set 08, 2009 21:41
- 6 Respostas
- 3493 Exibições
- Última mensagem por GABRIELA

Qua Set 09, 2009 18:52
Matrizes e Determinantes
-
- Sistemas
por GABRIELA » Qua Set 09, 2009 18:59
- 2 Respostas
- 1718 Exibições
- Última mensagem por GABRIELA

Qui Set 10, 2009 17:08
Sistemas de Equações
-
- Sistemas
por Douglaspimentel » Qui Abr 15, 2010 18:39
- 1 Respostas
- 2425 Exibições
- Última mensagem por Elcioschin

Qui Abr 15, 2010 20:14
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
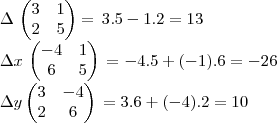
 encontrei, mas o
encontrei, mas o 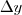 não esta correto. Onde está meu erro?
não esta correto. Onde está meu erro?
 está com as colunas trocadas. Refaça invertendo-as. A resposta que você irá obter é 26.
está com as colunas trocadas. Refaça invertendo-as. A resposta que você irá obter é 26.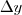 está montado corretamente, só que na hora de você fazer as operações está se condundindo:
está montado corretamente, só que na hora de você fazer as operações está se condundindo:
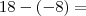
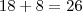


está com as colunas trocadas. Refaça invertendo-as. A resposta que você irá obter é 26.
está montado corretamente, só que na hora de você fazer as operações está se condundindo:

 mesmo:
mesmo: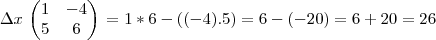


mesmo:
 , na apostila ensina a fazer o inverso como tinha feito naprimeira vez.Ai acho as respostas igual lá.
, na apostila ensina a fazer o inverso como tinha feito naprimeira vez.Ai acho as respostas igual lá.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.