 por inkz » Ter Nov 20, 2012 01:14
por inkz » Ter Nov 20, 2012 01:14
oi amigos, estou resolvendo provas antigas para me preparar para a p1 de cálculo 2, porém, não tenho as respostas. podem me ajudar, só conferindo se o raciocínio está correto? thx

1) Esboce a trajetória da curva gama(t) = ( e^t, e^(2t) )
como fiz:
x=e^t
y=e^2t
y=(e^t)^2 = x^2
então, a trajetória da curva gama(t) está contida na parábola y=x², porém apenas no primeiro quadrante, já que a imagem de gama(t) é maior ou igual a zero, para qualquer (t) pertencente ao seu domínio...
é isso mesmo?
valeeu =]
-
inkz
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Nov 20, 2012 01:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por MarceloFantini » Ter Nov 20, 2012 01:37
por MarceloFantini » Ter Nov 20, 2012 01:37
Na verdade o que você quis dizer é que a imagem de
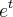
é maior que zero. Lembre-se que a exponencial nunca se anula e é sempre positiva.
Sua conclusão sobre estar contida na parábola está correta: ela estará contida na parábola mais precisamente com
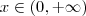
, ou seja, a parábola chega arbitrariamente próximo de zero, mas nunca é zero, e vai para infinito.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por inkz » Ter Nov 20, 2012 01:52
por inkz » Ter Nov 20, 2012 01:52
ops, tem razão. no papel eu havia colocado corretamente. foi erro meu ao transpor para cá. muito obrigado pela resposta amigo!!
-
inkz
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Nov 20, 2012 01:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo 1] Esboço de curvas
por rafaelbr91 » Sáb Mai 12, 2012 19:32
- 1 Respostas
- 2425 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 09:18
Cálculo: Limites, Derivadas e Integrais
-
- Trajetória da mosca
por Cleyson007 » Sex Ago 05, 2011 12:02
- 4 Respostas
- 5274 Exibições
- Última mensagem por FilipeCaceres

Sex Ago 05, 2011 16:05
Dúvidas Pendentes (aguardando novos colaboradores)
-
- [Trajetória da Curva - Sentido de Percurso]
por raimundoocjr » Ter Set 24, 2013 20:47
- 1 Respostas
- 1657 Exibições
- Última mensagem por Russman

Ter Set 24, 2013 21:54
Cálculo: Limites, Derivadas e Integrais
-
- Esboço do gráfico
por Dan » Sex Out 02, 2009 09:07
- 1 Respostas
- 3634 Exibições
- Última mensagem por admin

Sex Out 02, 2009 09:26
Cálculo: Limites, Derivadas e Integrais
-
- Esboço de gráficos.
por matematicouff » Sex Jun 22, 2012 19:02
- 1 Respostas
- 1593 Exibições
- Última mensagem por MarceloFantini

Dom Jun 24, 2012 02:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



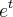 é maior que zero. Lembre-se que a exponencial nunca se anula e é sempre positiva.
é maior que zero. Lembre-se que a exponencial nunca se anula e é sempre positiva.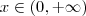 , ou seja, a parábola chega arbitrariamente próximo de zero, mas nunca é zero, e vai para infinito.
, ou seja, a parábola chega arbitrariamente próximo de zero, mas nunca é zero, e vai para infinito.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.