 por carlosecc » Seg Nov 19, 2012 21:55
por carlosecc » Seg Nov 19, 2012 21:55
Prezados queria umas dicas para achar a formula do somatorio de cada termo, a formula recursiva entendi tranquilo, mas quando a formula do somatorio eu fico remando sem sair do lugar uma sequencia que fiquei tentado achar é <2, 7, 12, 17, 22, ...>. Desde ja agradeço a quem responder.
-
carlosecc
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Nov 19, 2012 21:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informatica
- Andamento: cursando
 por MarceloFantini » Seg Nov 19, 2012 23:00
por MarceloFantini » Seg Nov 19, 2012 23:00
Isto é uma progressão aritmética, que por definição é uma sequência cuja diferença entre os termos é constante.
Para ver isto, note que
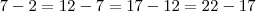
e assim em diante.
Não tenho tempo de fazer a dedução, mas o cálculo da soma é
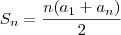
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por carlosecc » Ter Nov 20, 2012 20:41
por carlosecc » Ter Nov 20, 2012 20:41
Obrigado Marcelo irei tentar aplicar no exercicio, mas ta dificil aplicar somatorio sobre recursividade.
-
carlosecc
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Nov 19, 2012 21:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informatica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Transformar somatorio em formula
por guisantogui » Qua Mar 31, 2010 09:23
- 0 Respostas
- 3171 Exibições
- Última mensagem por guisantogui

Qua Mar 31, 2010 09:23
Progressões
-
- CLASSIFICAR CADA ITEM
por maykonnunes » Seg Mai 30, 2011 23:00
- 4 Respostas
- 2710 Exibições
- Última mensagem por maykonnunes

Sex Jun 10, 2011 15:15
Polinômios
-
- ufsm-se cada ratazana
por Natalie » Sex Set 16, 2011 17:28
- 3 Respostas
- 3404 Exibições
- Última mensagem por MarceloFantini

Sex Set 16, 2011 18:15
Progressões
-
- Bala para cada neto
por andersonsouza » Seg Fev 11, 2013 16:01
- 4 Respostas
- 3062 Exibições
- Última mensagem por andersonsouza

Seg Fev 11, 2013 23:24
Aritmética
-
- para cada vetor V o simétrico -V é único
por dkiwilson » Sáb Set 23, 2017 19:16
- 0 Respostas
- 2594 Exibições
- Última mensagem por dkiwilson

Sáb Set 23, 2017 19:16
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



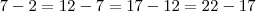 e assim em diante.
e assim em diante.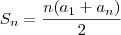 .
.



 .
.



