por SCHOOLGIRL+T » Qua Nov 07, 2012 21:05
por SCHOOLGIRL+T » Qua Nov 07, 2012 21:05
O gráfico da função f(x) = x²+ax+a+1 tem um valor mínimo igual a zero. O produto dos possíveis valores de a é:?
a) -1
b) -2
c) -3
d) -4
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Nov 17, 2012 17:58
por DanielFerreira » Sáb Nov 17, 2012 17:58
SCHOOLGIRL+T escreveu:O gráfico da função
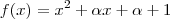
tem um valor mínimo igual a zero. O produto dos possíveis valores de

é:?
a) -1
b) -2
c) -3
d) -4
Sabemos que o vértice é dado por
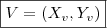
, onde

.
De acordo com o enunciado, temos

, então:
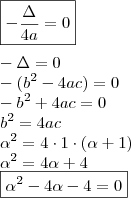
O produto é dado por
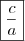
, então:
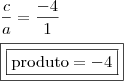 Schoolgirl+t
Schoolgirl+t,
troquei o

da sua função por

apenas para evitar 'confusão' com...
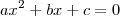
Comente qualquer dúvida!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5214 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4339 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5437 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3337 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2837 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



tem um valor mínimo igual a zero. O produto dos possíveis valores de
é:?
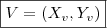 , onde
, onde .
. , então:
, então: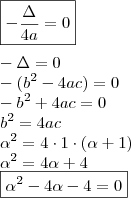
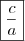 , então:
, então: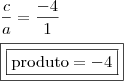
 da sua função por
da sua função por  apenas para evitar 'confusão' com...
apenas para evitar 'confusão' com...