 por SILMARAKNETSCH » Qua Nov 14, 2012 14:47
por SILMARAKNETSCH » Qua Nov 14, 2012 14:47
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por SILMARAKNETSCH » Qua Nov 14, 2012 14:49
por SILMARAKNETSCH » Qua Nov 14, 2012 14:49
SILMARAKNETSCH escreveu:
como derivar ? com raiz ? alguem pode ensinar o passo a passo? agradeço antecipadamente.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por e8group » Qua Nov 14, 2012 17:31
por e8group » Qua Nov 14, 2012 17:31
Generalizando , sempre que você depara com uma raiz de índice n , isto é
![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png)
, você pode escrever
![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png)
como
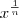
,
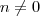
. Para derivar , a regra é a mesma que
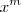
. .
Assim ,
![\boxed{ ( \sqrt[n]{x} ) ' = ( x^{\frac{1}{n} } )' = \frac{1}{n} \cdot x^{\frac{1}{n} - 1} = \frac{1}{n} \cdot x^{ \frac{1}{n} - 1 \cdot \frac{n}{n} } = \frac{1}{n} \cdot x^{\frac{ 1 - n}{n} } } \boxed{ ( \sqrt[n]{x} ) ' = ( x^{\frac{1}{n} } )' = \frac{1}{n} \cdot x^{\frac{1}{n} - 1} = \frac{1}{n} \cdot x^{ \frac{1}{n} - 1 \cdot \frac{n}{n} } = \frac{1}{n} \cdot x^{\frac{ 1 - n}{n} } }](/latexrender/pictures/06a85d3b9d47bd67445e6b2b02ad70dd.png)
.
Tente aplicar isto a este exercício , se você não conseguir post algo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por SILMARAKNETSCH » Qua Nov 14, 2012 17:47
por SILMARAKNETSCH » Qua Nov 14, 2012 17:47
santhiago escreveu:Generalizando , sempre que você depara com uma raiz de índice n , isto é
![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png)
, você pode escrever
![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png)
como
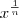
,
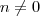
. Para derivar , a regra é a mesma que
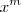
. .
Assim ,
![\boxed{ ( \sqrt[n]{x} ) ' = ( x^{\frac{1}{n} } )' = \frac{1}{n} \cdot x^{\frac{1}{n} - 1} = \frac{1}{n} \cdot x^{ \frac{1}{n} - 1 \cdot \frac{n}{n} } = \frac{1}{n} \cdot x^{\frac{ 1 - n}{n} } } \boxed{ ( \sqrt[n]{x} ) ' = ( x^{\frac{1}{n} } )' = \frac{1}{n} \cdot x^{\frac{1}{n} - 1} = \frac{1}{n} \cdot x^{ \frac{1}{n} - 1 \cdot \frac{n}{n} } = \frac{1}{n} \cdot x^{\frac{ 1 - n}{n} } }](/latexrender/pictures/06a85d3b9d47bd67445e6b2b02ad70dd.png)
.
Tente aplicar isto a este exercício , se você não conseguir post algo .
nossa fiquei confusa con o n e m e essa formula inteira é apenas para a minha primeira raiz do exercício? depois que entra o +x³?
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por SILMARAKNETSCH » Qua Nov 14, 2012 17:58
por SILMARAKNETSCH » Qua Nov 14, 2012 17:58
nossa santhiago parece que to vendo grego só com a fórmula não sei aplicar nela.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por e8group » Qua Nov 14, 2012 18:37
por e8group » Qua Nov 14, 2012 18:37
Ok . Vamos por partes ,
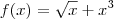

daí ,
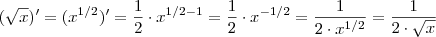
.
Já ,
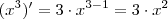
Ou seja ,
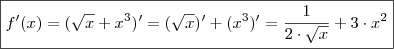
Por favor , se a dúvida permanecer , post algo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por SILMARAKNETSCH » Qua Nov 14, 2012 19:03
por SILMARAKNETSCH » Qua Nov 14, 2012 19:03
puxa vida obrigado en funções eu coloquei um recado que gostaria que vc fosse ler se possível é um agradecimento de tanto que este site fez por mim no caso vcs colaboradores.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14806 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Achar a derivada de uma função
por caiofisico » Seg Set 05, 2011 20:18
- 4 Respostas
- 3852 Exibições
- Última mensagem por caiofisico

Ter Set 06, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
-
- ]Derivada de uma função] derivada com raiz
por Leandro_Araujo » Ter Mar 06, 2012 01:11
- 5 Respostas
- 8561 Exibições
- Última mensagem por LuizAquino

Ter Mar 06, 2012 13:40
Cálculo: Limites, Derivadas e Integrais
-
- derivada de uma função
por jmario » Sex Mai 07, 2010 13:51
- 4 Respostas
- 3803 Exibições
- Última mensagem por Elcioschin

Sex Mai 07, 2010 23:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png) , você pode escrever
, você pode escrever ![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png) como
como 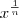 ,
, 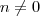 . Para derivar , a regra é a mesma que
. Para derivar , a regra é a mesma que 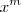 . .
. . ![\boxed{ ( \sqrt[n]{x} ) ' = ( x^{\frac{1}{n} } )' = \frac{1}{n} \cdot x^{\frac{1}{n} - 1} = \frac{1}{n} \cdot x^{ \frac{1}{n} - 1 \cdot \frac{n}{n} } = \frac{1}{n} \cdot x^{\frac{ 1 - n}{n} } } \boxed{ ( \sqrt[n]{x} ) ' = ( x^{\frac{1}{n} } )' = \frac{1}{n} \cdot x^{\frac{1}{n} - 1} = \frac{1}{n} \cdot x^{ \frac{1}{n} - 1 \cdot \frac{n}{n} } = \frac{1}{n} \cdot x^{\frac{ 1 - n}{n} } }](/latexrender/pictures/06a85d3b9d47bd67445e6b2b02ad70dd.png) .
. 
, você pode escrever
como
,
. Para derivar , a regra é a mesma que
. .
.


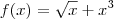
 daí ,
daí , 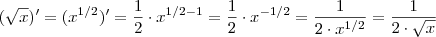 .
. 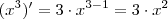
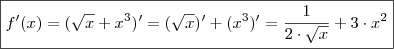


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.