 por Sherminator » Ter Nov 13, 2012 14:39
por Sherminator » Ter Nov 13, 2012 14:39
Boa tarde,
podiam-me ajudar a derivar 2 funções se faz favor?
A primeira é

qual é a sua derivada e como lá chegamos?
A segunda é
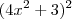
qual a sua derivada e como lá chegamos?
Agradeço a ajuda, um abraço!
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por e8group » Ter Nov 13, 2012 15:28
por e8group » Ter Nov 13, 2012 15:28
Perceba se
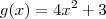
e
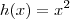
.Considerando
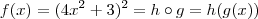
. Pela regra da cadeia , temos que
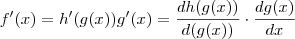
. Derivando em relação a x cada uma ,
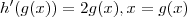
e
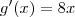
.Ou seja ,
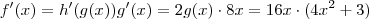
.
Tente fazer a outra , caso não conseguir post aqui .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Sherminator » Qua Nov 14, 2012 08:14
por Sherminator » Qua Nov 14, 2012 08:14
Obrigado pela ajuda, assim já consegui resolver a outra, deixo aqui a resolução a ver se está bem:

Podemos resolver pela formula
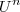
Assim:

Resultado:
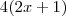
Correto?
Cumprimentos

-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por e8group » Qua Nov 14, 2012 09:43
por e8group » Qua Nov 14, 2012 09:43
sim estar certo . O que você fez , foi isto :
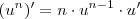
. No caso u é uma função .Isso mesmo.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Mínimo de função
por vinisoares9 » Dom Jun 24, 2012 00:22
- 2 Respostas
- 1780 Exibições
- Última mensagem por vinisoares9

Dom Jun 24, 2012 02:58
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Função diferenciável
por fff » Sáb Set 27, 2014 18:31
- 0 Respostas
- 1137 Exibições
- Última mensagem por fff

Sáb Set 27, 2014 18:31
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivada da função
por neoreload » Sáb Nov 01, 2014 08:25
- 5 Respostas
- 3596 Exibições
- Última mensagem por young_jedi

Dom Nov 02, 2014 10:29
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas]Domínio da função
por Laisa » Seg Mar 04, 2019 16:22
- 0 Respostas
- 4698 Exibições
- Última mensagem por Laisa

Seg Mar 04, 2019 16:22
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Esboço do gráfico de uma função
por Leon » Sáb Jun 07, 2014 22:28
- 0 Respostas
- 1088 Exibições
- Última mensagem por Leon

Sáb Jun 07, 2014 22:28
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 qual é a sua derivada e como lá chegamos?
qual é a sua derivada e como lá chegamos?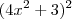 qual a sua derivada e como lá chegamos?
qual a sua derivada e como lá chegamos?
 qual é a sua derivada e como lá chegamos?
qual é a sua derivada e como lá chegamos?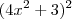 qual a sua derivada e como lá chegamos?
qual a sua derivada e como lá chegamos?
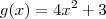 e
e 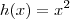 .Considerando
.Considerando 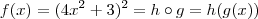 . Pela regra da cadeia , temos que
. Pela regra da cadeia , temos que 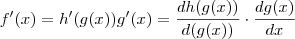 . Derivando em relação a x cada uma ,
. Derivando em relação a x cada uma , 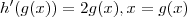 e
e 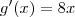 .Ou seja ,
.Ou seja , 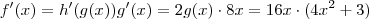 .
.

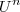

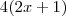


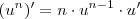 . No caso u é uma função .Isso mesmo.
. No caso u é uma função .Isso mesmo.

 .
.



