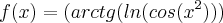 ?
?Não estou a conseguir...

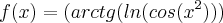 ?
?
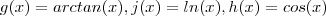 e
e 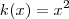 podemos rescrever
podemos rescrever  como ,
como , 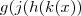 .
. ![f'(x) = [ g(j(h(k(x) )] ' = g' (j(h(k(x) ) \cdot j'(h(k(x)) \cdot h'( k(x) ) \cdot k'(x) f'(x) = [ g(j(h(k(x) )] ' = g' (j(h(k(x) ) \cdot j'(h(k(x)) \cdot h'( k(x) ) \cdot k'(x)](/latexrender/pictures/63bd9456be81f44fc49fc87a6f2306d2.png)
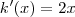
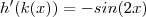
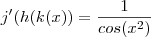
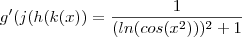
![f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x](/latexrender/pictures/aea40ffb897a36b26b98e11c3db3783f.png)

santhiago escreveu:Nestes casos eu gosto de decompor a função por composição .considerando ,e
podemos rescrever
como ,
.
Daí ,
Derivando cada uma em relação a x ,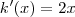
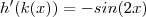
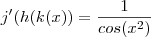
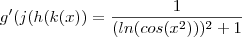
conclusão ,![f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x](/latexrender/pictures/aea40ffb897a36b26b98e11c3db3783f.png)
Por favor , comente qualquer dúvida .


Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)