 por GabrielMoreira » Sex Nov 09, 2012 23:56
por GabrielMoreira » Sex Nov 09, 2012 23:56
A questao diz o seguinte: A razão entre área de um quadrado inscrito em um semi-circulo de raio R e a de um outro quadrado inscito em um circulo de mesmo raio é:
A) 3/4
B)1/4
C)1/2
D)2/3
E)2/5
RESPOSTA: letra E
Fiz a relação de poligonos inscritos, sei que o quadrado inscrito no circulo tem lado valendo R.raiz quadrada de 2, não sei como relacionar o raio R do semi-circulo ao lado do quadrado inscrito nele
-
GabrielMoreira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Nov 09, 2012 23:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Nov 10, 2012 00:04
por DanielFerreira » Sáb Nov 10, 2012 00:04
GabrielMoreira,
seja bem-vindo!
Achei opção "b". Vou rever meus cálculos!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por GabrielMoreira » Sáb Nov 10, 2012 00:10
por GabrielMoreira » Sáb Nov 10, 2012 00:10
Obrigado! Quando se faz um desenho da questão a impressão que eu tive foi a letra B tambem, mas isso foi apenas no desenho, como nao me baseei em nenhum metodo ou calculo, nem citei. Segundo o gabarito oficial é a letra E
-
GabrielMoreira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Nov 09, 2012 23:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Nov 10, 2012 01:03
por DanielFerreira » Sáb Nov 10, 2012 01:03
Semi-circulo:
lado: l
raio: R
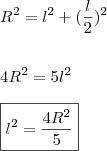 Círculo
Círculo:
lado: L
raio: R
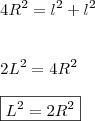
Daí,
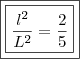
Depois posto a figura!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por GabrielMoreira » Sáb Nov 10, 2012 13:13
por GabrielMoreira » Sáb Nov 10, 2012 13:13
Muito Obrigado. Quanto a relação
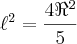
. Eu não conhecia. Existem formulas ou desenvolvimentos que eu deveria saber sobre poligonos inscritos em semi-circulos?
-
GabrielMoreira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Nov 09, 2012 23:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Nov 10, 2012 21:16
por DanielFerreira » Sáb Nov 10, 2012 21:16
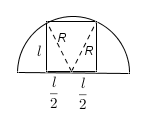
- semi.png (3.09 KiB) Exibido 3686 vezes
Aplicando o Teorema de Pitágoras...
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por GabrielMoreira » Sáb Nov 10, 2012 23:50
por GabrielMoreira » Sáb Nov 10, 2012 23:50
Entendi. Muito obrigado!!

-
GabrielMoreira
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Nov 09, 2012 23:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Nov 11, 2012 13:24
por DanielFerreira » Dom Nov 11, 2012 13:24
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [ANALISE COMBINATORIA] CMBH 2009
por GabrielMoreira » Dom Nov 11, 2012 00:15
- 5 Respostas
- 2975 Exibições
- Última mensagem por DanielFerreira

Qua Nov 14, 2012 23:22
Análise Combinatória
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8726 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4721 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4829 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
-
- Geometria plana
 por Paulo A G » Qua Jan 26, 2011 16:11
por Paulo A G » Qua Jan 26, 2011 16:11
- 0 Respostas
- 2542 Exibições
- Última mensagem por Paulo A G

Qua Jan 26, 2011 16:11
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



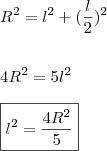
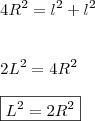
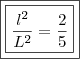
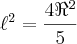 . Eu não conhecia. Existem formulas ou desenvolvimentos que eu deveria saber sobre poligonos inscritos em semi-circulos?
. Eu não conhecia. Existem formulas ou desenvolvimentos que eu deveria saber sobre poligonos inscritos em semi-circulos?
