Olá, a questão que estou desenvolvendo é a seguinte...
Uma revendedora de automóveis observou que, em determinado ano, a venda de veículos automáticos aumentava, mensalmente, segundo uma progressão aritmética de razão 50. Considerando-se que, em junho, foram vendidas
320 unidades, pode se afirmar que o numero de veículos automáticos comercializados pela revendedora,
nesse ano, foi igual a
01) 690
02) 1380
03) 2070
04) 4140
05) 8280
Resolvi da seguinte forma:
(r= 50) (a6= 320) (a12 e a1= ?)
descobrindo a12 pela formula geral
--> an = a1 + (n+1)r
a6 = a12 +(6-12).50
320 = a12 - 300
a12= 620
descobrindo a1:
a6 = a1 + (6-1).50
320 = a1 + 250
a1 = 30
Utilizei a formula da Soma de termos para saber a soma
dos valores de carros vendidos nos 12 meses...
--> Sn = (a1+an).n => (30+620).12 => Sn = 3900
..............2.................2
porém não confere com o resultado do gabarito... que é 4140
gostaria de ajuda na interpretação da questão ou no próprio cálculo...
______________________________________________Muito Obrigado!
______________________________________________Joedson Azevedo
____________________________________________________________
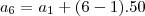
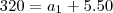
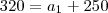
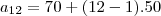
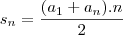
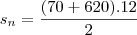
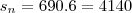
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)