 por SILMARAKNETSCH » Sex Nov 09, 2012 09:30
por SILMARAKNETSCH » Sex Nov 09, 2012 09:30
Lim x + 1
x - ² ---------
4x - 3
obs onde esta um traço em baixo de lim é a flexinha perdoem aprenderei a fazer corretamente
Editado pela última vez por
SILMARAKNETSCH em Sex Nov 09, 2012 09:34, em um total de 1 vez.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por SILMARAKNETSCH » Sex Nov 09, 2012 09:33
por SILMARAKNETSCH » Sex Nov 09, 2012 09:33
lim x+1
-------------
x - ² 4x - 3
este é o formato só em baixo do limite é que não consegui colocar a seta ainda não sei mexer com as fórmulas prontas
então a questão é na primeira linha x+1 e debaixo 4x - 3
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por e8group » Sex Nov 09, 2012 10:14
por e8group » Sex Nov 09, 2012 10:14
Utilizando latex , veja como fica o numerador e denominador
- Código: Selecionar todos
\frac{x+1}{x^2 - 4x - 3 }
, resultado :
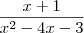
.
OBS. o Código deve estar entre
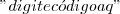
.
Para limites veja como fica ,
- Código: Selecionar todos
\lim_{x\to a }
. Resultado :
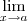
Como é iniciante , utilize este site
http://www.codecogs.com/latex/eqneditor.php?lang=pt-br , lá há um menu com as fórmulas que auxiliara vc até acostumar com o padrão . Além disso , automaticamente a medida que vc digitar os códigos lá será compilado em qual quer formato de imagem , (gif , png , etc ) .
Por favor ,corrija seu tópico para podermos ajudar vc .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sex Nov 09, 2012 10:19
por MarceloFantini » Sex Nov 09, 2012 10:19
Bom dia Silmara. Por favor tente usar LaTeX nas suas postagens. Se entendi bem, para este limite por exemplo o código seria
- Código: Selecionar todos
\lim_{x \to 2} \frac{x+1}{4x-3}
que nos dá
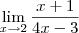
.
O resultado deste limite é direto, pois não temos indeterminações. Assim
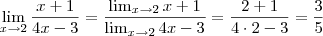
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por SILMARAKNETSCH » Sex Nov 09, 2012 12:08
por SILMARAKNETSCH » Sex Nov 09, 2012 12:08
agradeço demais depois vou tentar colocar mais alguns problemas que tem infinito para ver se consigo abraço!!! a maior caridade esta no ato de querer ajudar ganhei uma bolsa ENEM depois de 29 anos sem estudar faço administração mas a matemática esta sendo minha dificuldade se não aprender vou ficar de DP mas colocarei exercícios aqui e irei treinar trocando os numeros para estar fera na prova do fim do mes.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4793 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5126 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7267 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4446 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




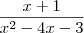 .
.  .
. 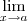

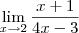 .
.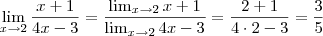 .
.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
