 por anneliesero » Qui Nov 08, 2012 16:21
por anneliesero » Qui Nov 08, 2012 16:21
Gente, porque a minha não está dando certo?
Eu fiz assim:
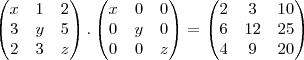
a11= 2x+0+0=2x=2 x=2
a22= 0+2y+0=2y=12 y=6
a33= 0+0+2z=20 z=10
A resposta certa é a B( 1,4,4)

(MACK) Sabe-se que
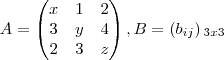
, é uma matriz diagonal, ou seja,

se i diferente j e
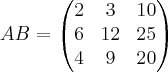
. Os valores de
x,
y e
z são respectivamente:
a) 2,3, 4
b)1, 4, 4
c) 7,7,7
d) 2,3,1
e)1,1,1
''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sáb Nov 24, 2012 09:25
por e8group » Sáb Nov 24, 2012 09:25
Veja que a segunda matriz à esquerda da igualdade é diagonal .Portanto , tomar o produto ,

é o mesmo que ,
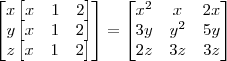
Basta achar condições para
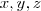
tal que os elementos da matriz à esquerda da igualdade sejam igual ao mesmo a direita da igualdade .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7168 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3576 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6728 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4704 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por Barbara » Ter Ago 18, 2009 15:26
- 4 Respostas
- 4814 Exibições
- Última mensagem por Molina

Qui Ago 20, 2009 18:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
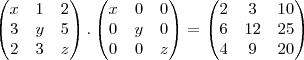

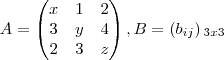 , é uma matriz diagonal, ou seja,
, é uma matriz diagonal, ou seja,  se i diferente j e
se i diferente j e 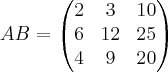 . Os valores de x, y e z são respectivamente:
. Os valores de x, y e z são respectivamente:


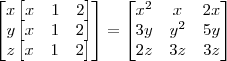
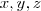 tal que os elementos da matriz à esquerda da igualdade sejam igual ao mesmo a direita da igualdade .
tal que os elementos da matriz à esquerda da igualdade sejam igual ao mesmo a direita da igualdade .