Sub-seção para materiais das disciplinas relacionadas ao Instituto de Física.
Utilize a área de pedidos para outros ou caso a sub-seção da disciplina ainda não possua material.
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos, bibliografias etc.
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Cleyson007 » Qua Nov 07, 2012 16:55
por Cleyson007 » Qua Nov 07, 2012 16:55
Uma bola de beisebol deixa o bastão do batedor com uma velocidade inicial de v
0 = 37,0m/s com um ângulo inicial de
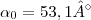
em um local onde g = 9,8 m/s².
a) Ache a posição da bola e o módulo, a direção e o sentido de sua velocidade para t = 2,0s.
b) Calcule o tempo que a bola leva para atingir a altura máxima de sua trajetória e ache a altura h nesse ponto.
c) Ache o
alcance horizontal R, ou seja, a distância entre o ponto inicial e o ponto onde a bola atinge o solo.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Neperiano » Qua Nov 07, 2012 17:01
por Neperiano » Qua Nov 07, 2012 17:01
Olá
Cleyson, vou fazer um pouco diferente de nosso colega antes, não vou resolver a questão como ele, mas vou tentar de dar as dicas.
Primeiro, desenhe a situação, nela você notará que haverá uma velocidade inicial inclinada a 53,1 com x, logo haverá uma velocidade em x, e uma em y. Certo?
A pergunta é achar a posição da bola, ai vem a grande questão, a posição em x ou em y? Na dúvida sempre calcule as duas, o que eu acho que deve fazer.
Lembrando que isto é movimento bidimensional.
Para calcular a posição em x, você precisará da equação:
x=xo+vx.t
Na qual você possui todos os valores, lembrando que você precisa transformar sua velocidade inicial, em vx e voy.
Quando calcular em y, deverá usar a equação:
y=yo+voy.t+(g.t^2)/2
Que novamente você tem todos os valores.
Depois é necessário o módulo da velocidade, o módulo da velocidade será o "pitagoras" da velocidade em x neste ponto e a velocidade em y neste ponto, como foi feito na questão anterior.
Vou deixar você tentar quebrar a cabeça agora, qualquer dúvida.
Att
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Cleyson007 » Qua Nov 07, 2012 17:27
por Cleyson007 » Qua Nov 07, 2012 17:27
Olá Neperiano!
A figura que ilustra a situação:

Minha dúvida é quanto ao ângulo que aparece no enunciado.. Qual fórmula? Como encontrá-la?
Fico te aguardando.
Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qua Nov 07, 2012 18:15
por MarceloFantini » Qua Nov 07, 2012 18:15
A velocidade horizontal da bola não muda, mas a velocidade vertical sim. As equações são
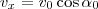
e
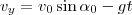
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Qua Nov 07, 2012 21:00
por Cleyson007 » Qua Nov 07, 2012 21:00
Minha dúvida é: Como foram encontradas essas equações?
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qua Nov 07, 2012 23:13
por MarceloFantini » Qua Nov 07, 2012 23:13
Decomponha o vetor nos eixos. Não há aceleração no eixo horizontal, mas há a aceleração na vertical devido á gravidade.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Qui Nov 08, 2012 15:05
por Cleyson007 » Qui Nov 08, 2012 15:05
Outra dúvida: Como calculo o alcance horizontal?
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qui Nov 08, 2012 17:00
por MarceloFantini » Qui Nov 08, 2012 17:00
A distância percorrida será
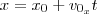
. Se ele partir da origem, temos

. Ele irá parar quando atingir o chão, ou seja, você precisa encontrar o instante em que a vertical se anula novamente. Achando este instante, basta substituir na equação e você terá a resposta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Física
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
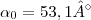 em um local onde g = 9,8 m/s².
em um local onde g = 9,8 m/s².



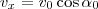 e
e 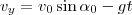 .
.

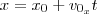 . Se ele partir da origem, temos
. Se ele partir da origem, temos  . Ele irá parar quando atingir o chão, ou seja, você precisa encontrar o instante em que a vertical se anula novamente. Achando este instante, basta substituir na equação e você terá a resposta.
. Ele irá parar quando atingir o chão, ou seja, você precisa encontrar o instante em que a vertical se anula novamente. Achando este instante, basta substituir na equação e você terá a resposta.

 , avisa que eu resolvo.
, avisa que eu resolvo.

