 por cristina » Seg Set 14, 2009 18:49
por cristina » Seg Set 14, 2009 18:49
Dado o triândulo ABC e sabendo que o lado a mede 16, o lado b mede 10 e o ângulo C formado por estes dois lados mede 60º,
quais são os valores dos outros elementos do triângulo (lado c e ângulos A e B).
o lado c eu achei pela lei dos cossenos, é isso mesmo????, dai a resposta c=14
mas não sei qual o metodo para achar os ângulos, preciso de ajuda
Grata pela colaboração....
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por Marcampucio » Seg Set 14, 2009 22:56
por Marcampucio » Seg Set 14, 2009 22:56
Agora você conhece os tres lados. Aplique novamente a lei dos cossenos com outro enfoque mantendo o cosseno do ângulo como incógnita.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por cristina » Seg Set 14, 2009 23:32
por cristina » Seg Set 14, 2009 23:32
Olá, obrigada....
Mas desta forma já tentei e não cheguei a nehum resultado...
poderia explicar melhor?
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por Marcampucio » Ter Set 15, 2009 00:19
por Marcampucio » Ter Set 15, 2009 00:19
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por cristina » Ter Set 15, 2009 09:27
por cristina » Ter Set 15, 2009 09:27
Olá obrigada, o meu estava em simplificar eu esqueci dessa parte, outra coisa...
como seu consigo chegar ao resultado de 1/7 a 82º , existe uma tabela?
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por Marcampucio » Ter Set 15, 2009 16:44
por Marcampucio » Ter Set 15, 2009 16:44
Olá,
se
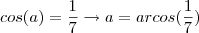
existe sim uma tabela trigonométrica que fornece esses valores, mas o que eu fiz (bem mais simples) foi usar uma calculadora.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6602 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- Triangulo
por ginrj » Ter Abr 28, 2009 20:58
- 3 Respostas
- 3793 Exibições
- Última mensagem por ginrj

Sáb Mai 02, 2009 12:30
Geometria Plana
-
- Triângulo.
por Molina » Qua Mai 13, 2009 23:20
- 2 Respostas
- 2153 Exibições
- Última mensagem por Molina

Qui Mai 14, 2009 19:04
Geometria Plana
-
- Triângulo
por Fogodc » Seg Abr 05, 2010 23:39
- 1 Respostas
- 1947 Exibições
- Última mensagem por Fogodc

Qua Abr 07, 2010 11:37
Geometria Plana
-
- triangulo
por geriane » Qui Abr 22, 2010 16:15
- 1 Respostas
- 1857 Exibições
- Última mensagem por MarceloFantini

Qui Abr 22, 2010 17:00
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




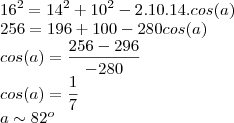
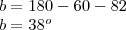
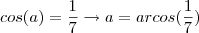


 , avisa que eu resolvo.
, avisa que eu resolvo.

