Determinar a equação da elipse que satisfaz as condições dadas:
centro
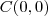 , focos no eixo dos x, excentricidade
, focos no eixo dos x, excentricidade 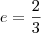 e passa pelo ponto
e passa pelo ponto 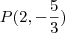 .
.Bom, sei que
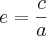 , portanto
, portanto  , então,
, então, 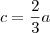
Em relação ao ponto dado, tentei substitui-lo em x e y na fórmula da elipse
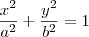 , e tirando o mmc, e isolando o
, e tirando o mmc, e isolando o 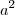 , obtive
, obtive 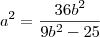
Como fazer esse exercício?


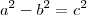
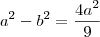
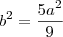
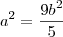
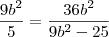
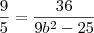
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)