 por menino de ouro » Ter Out 30, 2012 18:21
por menino de ouro » Ter Out 30, 2012 18:21
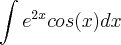
eu começei assim : chamei u de :
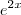
entao du =
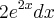
chamei dv : cos( x )dx então v = sen(x)
utilizando a formula da integral por partes (u)(dv):
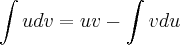
encontrei:
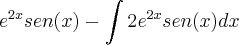
agora eu tenho que resolver a nova integral? correto? para que? ainda não sei direito o porque?
como continua esse exercicio ? eu sei que a resposta tem que dar :
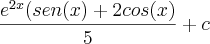
nao sei como chegar até aqui ,gostaria de aprender como que se resolve de uma maneira mais facil de entender! obrigado
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por MarceloFantini » Ter Out 30, 2012 21:00
por MarceloFantini » Ter Out 30, 2012 21:00
Sim, agora você tem que resolver
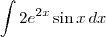
. Quando você resolver esta nova integral você voltará à integral original. A partir disso, você substitui a primitiva que encontrar, que terá a integral original, e resolva para encontrar a primitiva. Se não ficar muito claro, poste os novos cálculos que discutiremos passo a passo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por menino de ouro » Ter Out 30, 2012 22:26
por menino de ouro » Ter Out 30, 2012 22:26
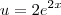
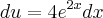
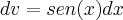
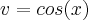
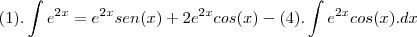
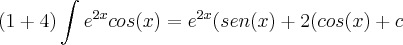
feito isso cheguei ao resultado esperado , acho que é isso?
obrigado!
vçe , sabe se existe algumas vídeo aulas (youtube, ou outro lugar ) que mostre exemplos de [ técnicas de integração-integraçao de potencias e produtos de funções trigonométricas?]
tipo :
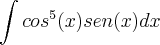
,
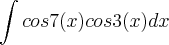
,
agradeço,Marcelo
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por MarceloFantini » Ter Out 30, 2012 22:39
por MarceloFantini » Ter Out 30, 2012 22:39
Você errou ao afirmar que
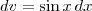
implica em

, pois na verdade é

. Devido ao sinal de menos na integral anterior eles cancelaram-se e você chegou na resposta certa, mas tome cuidado da próxima vez. No mais, está tudo correto.
Existem as vídeo-aulas do nosso colega
Luiz Aquino no Youtube, elas podem te ajudar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- TECNICAS DE INTEGRAÇÃO
por Marcio Cristo » Qui Dez 22, 2011 18:35
- 5 Respostas
- 3045 Exibições
- Última mensagem por LuizAquino

Sex Dez 23, 2011 18:00
Cálculo: Limites, Derivadas e Integrais
-
- Técnicas de integração
por Victor Mello » Seg Nov 18, 2013 23:04
- 2 Respostas
- 1659 Exibições
- Última mensagem por Victor Mello

Ter Nov 19, 2013 00:16
Cálculo: Limites, Derivadas e Integrais
-
- [Tecnicas de integraçao por substiuiçao simples]
por menino de ouro » Qua Out 24, 2012 16:12
- 1 Respostas
- 1508 Exibições
- Última mensagem por young_jedi

Qua Out 24, 2012 16:51
Cálculo: Limites, Derivadas e Integrais
-
- Técnicas de integração - multiplicando pelo fator unitário
por Victor Mello » Qui Nov 21, 2013 18:37
- 2 Respostas
- 1716 Exibições
- Última mensagem por Victor Mello

Qui Nov 21, 2013 23:27
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por Partes] Constante de integração
por KleinIll » Dom Set 01, 2019 14:11
- 2 Respostas
- 5956 Exibições
- Última mensagem por KleinIll

Sex Set 06, 2019 18:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
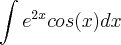
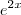 entao du =
entao du = 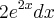 chamei dv : cos( x )dx então v = sen(x)
chamei dv : cos( x )dx então v = sen(x)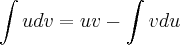
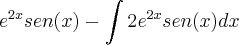 agora eu tenho que resolver a nova integral? correto? para que? ainda não sei direito o porque?
agora eu tenho que resolver a nova integral? correto? para que? ainda não sei direito o porque?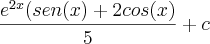


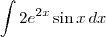 . Quando você resolver esta nova integral você voltará à integral original. A partir disso, você substitui a primitiva que encontrar, que terá a integral original, e resolva para encontrar a primitiva. Se não ficar muito claro, poste os novos cálculos que discutiremos passo a passo.
. Quando você resolver esta nova integral você voltará à integral original. A partir disso, você substitui a primitiva que encontrar, que terá a integral original, e resolva para encontrar a primitiva. Se não ficar muito claro, poste os novos cálculos que discutiremos passo a passo.

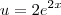
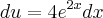
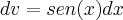
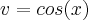
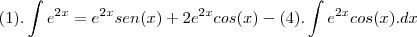
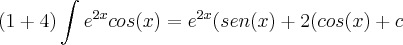
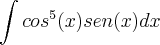 ,
, 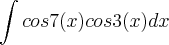 ,
,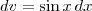 implica em
implica em  , pois na verdade é
, pois na verdade é  . Devido ao sinal de menos na integral anterior eles cancelaram-se e você chegou na resposta certa, mas tome cuidado da próxima vez. No mais, está tudo correto.
. Devido ao sinal de menos na integral anterior eles cancelaram-se e você chegou na resposta certa, mas tome cuidado da próxima vez. No mais, está tudo correto.